АЛГЕБРА 2022-2023 навчальний рік
Наснаги,успіхів,удачі!
ІІ семестр
26.05.23Контрольна робота( річна) 13.00-15.00
22.05-26.05.23
Рівняння що зводяться до алгебраїчних
Приєднайтесь до відео консультації за розкладомРозгляньте приклади
Рівняння що зводяться до алгебраїчних
Приєднайтесь до відео консультації за розкладомПередивіться запропоновані відео уроки
15.05-19.05.23Сам. робота дивись завдання нижчеРівняння що зводяться до алгебраїчних
Приєднайтесь до відео консультації за розкладомПередивіться запропоновані відео уроки
Самостійна робота №209(3),210(3),211(3) * додатково( окрема оцінка №211(5))Найпростіші тригонметричні рівняння.Приєднайтесь до відео консультації за розкладомПередивіться запропоновані відео уроки
Попрацюйте з теоритичними відомостями
Рівняння називається тригонометричним, якщо невідома величина знаходиться під знаком тригонометричних функцій. Найпростішими тригонометричними рівняннями називаються рівняння 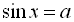 ,
, 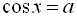 ,
, 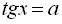 ,
, 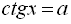 . Розв’язати найпростіше тригонометричне рівняння – означає знайти множину всіх кутів, що мають дане значення
. Розв’язати найпростіше тригонометричне рівняння – означає знайти множину всіх кутів, що мають дане значення 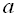 тригонометричної функції. Якщо тригонометричне рівняння не є найпростішим, то за допомогою тотожних перетворень його треба звести до одного або кількох найпростіших, розв’язання яких визначається стандартними формулами.
тригонометричної функції. Якщо тригонометричне рівняння не є найпростішим, то за допомогою тотожних перетворень його треба звести до одного або кількох найпростіших, розв’язання яких визначається стандартними формулами.
При використанні формул для розв’язування тригонометричних рівнянь враховуйте, що
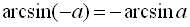 ;
; 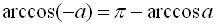 ;
;
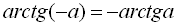 ;
; 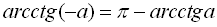 .
.
Рогляньте приклади
Рівняння називається тригонометричним, якщо невідома величина знаходиться під знаком тригонометричних функцій. Найпростішими тригонометричними рівняннями називаються рівняння ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Розв’язати найпростіше тригонометричне рівняння – означає знайти множину всіх кутів, що мають дане значення
. Розв’язати найпростіше тригонометричне рівняння – означає знайти множину всіх кутів, що мають дане значення ![]() тригонометричної функції. Якщо тригонометричне рівняння не є найпростішим, то за допомогою тотожних перетворень його треба звести до одного або кількох найпростіших, розв’язання яких визначається стандартними формулами.
тригонометричної функції. Якщо тригонометричне рівняння не є найпростішим, то за допомогою тотожних перетворень його треба звести до одного або кількох найпростіших, розв’язання яких визначається стандартними формулами.
При використанні формул для розв’язування тригонометричних рівнянь враховуйте, що
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Рогляньте приклади
Виконайте завдання тестhttps://vseosvita.ua/test/start/rlv647
08.05-12.05.23
08.05 до 20.00 тествання https://vseosvita.ua/test/start/ehf554Обернені тригонометричні функції.Приєднайтесь до відео консультації за розкладомПопрацюйте з теоритичними відомостями та випишіть у зошит всі необхідні формули
11.05Виконайте завдання:№1074,1075,1088(1,3)
Подивіться
01.05-05.05.23Формули перетворення суми та різниці у добутокПриєднайтесь до відео консультації за розкладомПопрацюйте з теоритичними відомостямиРозгляьте прикладиФОРМУЛИ ПЕРЕТВОРННЯ ДОБТКУ У СУМУ, АО РІЗНИЦЮ
Виконайте завдання:№1 тестування 02.05 14.00-15.00№2 Контрольна робота
24.04-28.04.23
Формули половинного аргументуПриєднайтесь до відео консультації за розкладомПопрацюйте з теоритичними відомостями
Випишіть у зошит всі формули половинного аргументуВиконайте завданняТестування https://vseosvita.ua/test/start/bmh626відповіді записувати звичайним дробом, час тестування 25 хвилин.
24.04.23 Використання формул додавання, подвійного кута,половинного кута.Приєднайтесь до відео консультації за розкладомПопрацюйте з теоритичними відомостямиВиконайте завдання: 1-7
1
2
3
4
5
6
7
17.04-21.04.2320.04Доведіть формули потрійного аргументуТест №1 Формули додавання ( 14.00-15.00 18.04)
Тест №2 Формули зведення 18.04
Формули зведення.Формули додавання, подвійного кута,половинного кута.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
|
|
|
|
|
|
Розгляньте прикладиВиконайте завдання
18.04 тестування №1 №2
10.04-14.04.23Формули зведенняПриєднайтесь до відео консультації за розкладомПопрацюйте з теоритичними відомостямиРозгляньте приклади
Виконайте завдання: виконуючи номери пишіть номери прикладів№869 - 6 б №873 приклади 1,2, 3,7 по 1б 4, 5,6 по 2 б
Виконайте завдання: виконуючи номери пишіть номери прикладів
Основні тригонометричні тотожностіПриєднайтесь до відео консультації за розкладомПодивіться відео урок
Попрацюйте з теоритичними відомостямиЗавдання !вирази такого виду записувати так: "синус квадрат альфа" Тестування https://vseosvita.ua/test/start/drl717
Попрацюйте з теоритичними відомостями
03.04-07.04.2306.04 тестуванняПопрацюйте з теоритичними відомостями, прикладами,відео уроками

Перейдіть до тестування( час тестування 25 хвилин)
Властивості графіків тангенс та котангенс.Приєднайтесь до відео консультації за розкладомПодивіться відео урок
Теоритичні відомостіРозгляньте приклади
Виконайте завдання:№792(1), 793(5)
Теоритичні відомості
Виконайте завдання:
20.03-24.03.23
Властивості графіків синус та косинусПобудувати графік 8 б
Періодичні функціїПриєднайтесь до відео консультації за розкладомПодивіться відео урок
Теоритичні відомості
Завдання :Самостійна робота до 15.00№738(3,6,9) 740(б)743(2,4,6)
Тригонометричні функції числового аргументу.Знаки тригонометричних функцій.Парність та непарнасть.Приєднайтесь до відео консультації за розкладомПодивіться відео урокВиконайте завдання 20.03 тестування https://vseosvita.ua/test/start/pjq863
Теоритичні відомості
13.03-17.03.23Тригонометричні функції числового аргументуПриєднайтесь до відео консультації за розкладомПодивіться відео урок
Повторення"Радіанне вимірювання кутів"Приєднайтесь до відео консультації за розкладомПодивіться відео урок
Попрацюйте з теоритичними відомостями
Повторення
Попрацюйте з теоритичними відомостями
06.03-10.03.23На цьому тиждні працюємо в асинхроні. З 13.03 будемо працювати синхронноВиконуємо завдання з теми ірраціональні рівняння та нерівності,повторюємо теоритичні відомості. переглядаємо відео уроки.
"Ірраціональні рівняння та нерівності."Відео уроки
Попрацюйте з параграфом підручникаОсновні відомості
Розгляньте приклади
Тестування https://vseosvita.ua/test/start/pcd591 тривалість тестування 15 хвилин Контрольна робота
27.02-03.03.23
"Ірраціональні нерівності"
20.02-24.02.2321.02 Самостійна робота 14.00-15.00Достатній рівень 8б
"Ірраціональні нерівності"
13.02-17.02.23"Системи ірраціональних рівнянь"
06.02-09.02.23
Різні методи розв'язування ірраціональних рівнянь"07.02 23 сам.робота№1 тестування№2 самостійна робота№3 №637,638
Відео урок
Завдання:
30.01-03.02. 2023

23.01-27.01. 2023
№3 тестуванняhttps://vseosvita.ua/test/start/bxb672
Приєднайтесь до відео консультацій за розкладом
Передивіться відео уроки
Теоритичні відомості
№3 тестуванняhttps://vseosvita.ua/test/start/bxb672
16.01-20.01 2023
"Перетворення виразів з коренями п-ного степеня"
Приєднайтесь до відео консультацій за розкладом
Передивіться відео уроки
Опрацюйте теоритичні відомості
Розгляньте прикладиЗавдання №1 №522,525 до19.01 19.01 максимальний бал 11до 23.01 максимальний бал 8далі максимальний бал 6
09.01-13.01 2023
"Означення кореня п-ного степеня.Властивості кореня п-ного степеня"
10.01 Самостійна робота. Відповіді надсилати електронною поштою
оцінюваннядо 15.00 максимальний бал 10сьогодні максимальний бал 8далі максимальний бал 6
Виконуєммо завдання №1,№2
Приєднайтесь до відео консультацій за розкладом
Опрацюйте теоритичні відомості



Нерівності з параметром.Приєднайтесь до відео консультацій за розкладомПередивіться запропановані відео уроки
Попрацюйте з теоритичними відомостями
№3
14.11-18.11.2022
Самостійна робота:( завдання дивись у розділі "Виконай завдання")
Приєднайтесь до відео консультації за розкладом
Передивіться відео уроки
07.11-11.11.2022
Приєднайтесь до відео консультації за розкладом
Передивіться відео уроки
24.10-28.10 2022
Узагальнення.
27.10 10-В 11.00 Контрольна робота.
Приєднайтесь до відео консультації за розкладом
Передивіться відео уроки
Передивіться приклади класної роботи.17.10-21.10 2022
"Розв'язування нерівностей.Метод інтервалів."Увага!!!Теорема Безу
відео https://www.youtube.com/watch?v=XSWiDZAjz88
презентація
Приєднайтесь до відео консультації за розкладомПередивіться відео уроки
Повторіть застосування методу інтервалів на прикладах.№1 ( до 19.10)
№258(4)259(2) №262(2) 263(5)
Повторіть застосування методу інтервалів на прикладах.
10.10-14.10 2022
Скористайтесь корисними підказками
1. Схема розв’язування нерівності методом
інтервалів :
1. Привести нерівність до такого виду, де в
лівій частині знаходиться функція, а в правій 0.
2. Знайти область визначення функції.
3. Знайти нулі функції, тобто - вирішити
рівняння, х1 = m, x2 = n.
4. На числову пряму нанесемо область визначення функції і за допомогою нулів розіб’ємо її (область визначення) на інтервали.
5. Визначити знаки функції на отриманих
інтервалах.
6. Вибрати інтервали, де функція набуває
необхідних значень і записати відповідь.

2. Застосування методу інтервалів на прикладах.
Методичний прийом „Працюємо за зразком”. Разом з учнями розв’язуємо нерівність методом інтервалів з коментуванням.
а) Розв’яжемо
нерівність (х + 2)(х - 3)(х - 5) >0.
; (-2; 3); (3; 5); (5; +
Відповідь: (-2; 3) (5; +
На кожному з проміжків
функція зберігає знак, а після переходу через нулі її знак змінюється. У такий
спосіб можна знайти знаки функції виду
f(x)
= (х
– х1)(х – х2)(х – х3)…(х - хn)
б) Розв’яжемо
нерівність 3х2 – 6х + 24 <
0.
Зведемо нерівність до нерівності виду: 3(х +
2)(х - 4)
х1 =
-2, нулі функції
Позначимо на координатній прямій нулі функції, розіб’ємо її на інтервали
Відповідь: (-2; 4).
в) Розв’язування
дробових раціональних нерівностей.
Метод інтервалів можна
застосовувати і для розв’язування дробових нерівностей. Дробово-раціональна
функція може міняти знак тільки в тих точках, в яких вона дорівнює нулю або не
існує.
Розв’язання:
D(f): хє всі числа крім 15
Нулі функції: х1 =-15,
х2 = 2
Наносимо на
координатний промінь нулі функції і ОДЗ, визначимо знак функції на отриманих
інтервалах, виберемо інтервал, де функція набуває додатних значень.
Відповідь:
https://vseosvita.ua/test/start/cns253
Контрольна робота 10-В

03.10-07.10. 2022
"Властивості і графіки основних видів функцій.Перетворення графіків."
| Преобразование y = f (x + c), где c – число | |
В случае c > 0 график функции y = f (x) переносится влево на расстояние | c | | 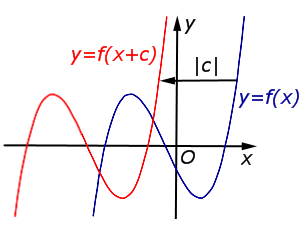 |
В случае c < 0 график функции y = f (x) переносится вправо на расстояние | c | | 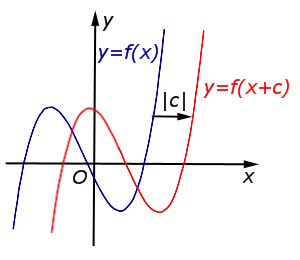 |
| Преобразование y = f (x) + c, где c – число | |
В случае c > 0 график функции y = f (x) переносится вверх на расстояние | c | |  |
В случае c < 0 график функции y = f (x) переносится вниз на расстояние | c | | 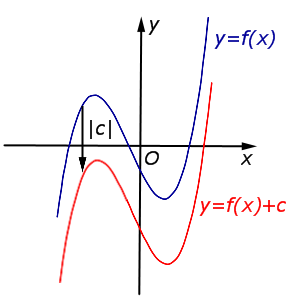 |
| Преобразование y = – f (x) | |
График функции y = f (x) симметрично отражается относительно оси Ox. | 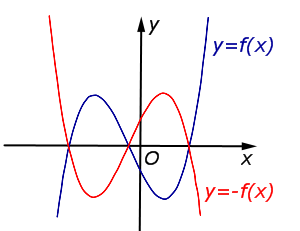 |
| Преобразование y = f ( – x) | |
График функции y = f (x) симметрично отражается относительно оси Oy. | 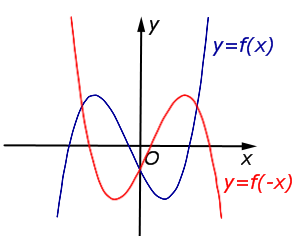 |
| Преобразование y = f (kx), где k – число | |
В случае k > 1 происходит сжатие графика функции | 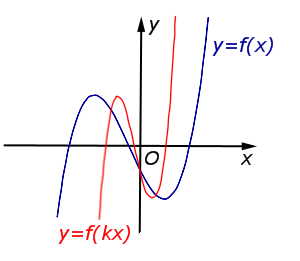 |
В случае 0 < k < 1 происходит растяжение графика функции y = f (x) в | 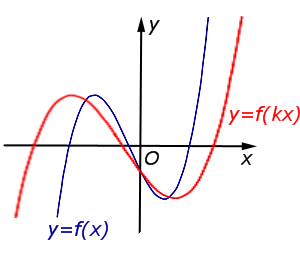 |
В случае – 1 < k < 0 происходит растяжение графика функции y = f (x) в | 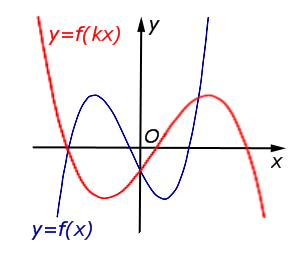 |
В случае k < – 1 происходит сжатие графика функции | 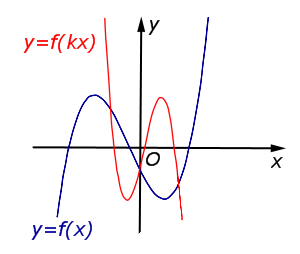 |
| Преобразование y = k f (x), где k – число | |
В случае k > 1 происходит растяжение графика функции y = f (x) в k раз от оси Ox. | 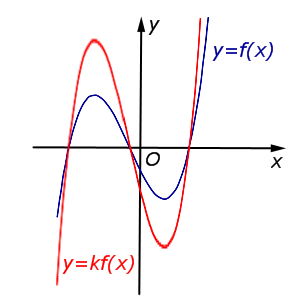 |
В случае 0 < k < 1 происходит сжатие графика функции y = f (x) в | 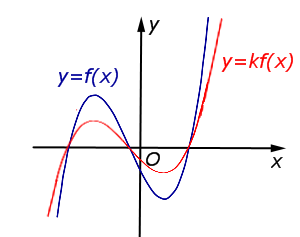 |
В случае – 1 < k < 0 происходит сжатие графика функции y = f (x) в | 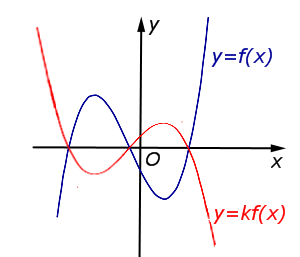 |
В случае k < – 1 происходит растяжение графика функции y = f (x) в | k | раз от оси Ox с последующим симметричным отражением графика относительно оси Ox. | 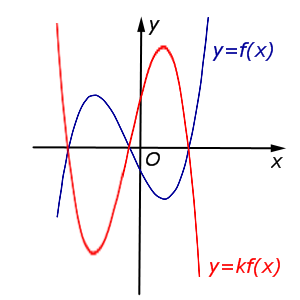 |
| Преобразование y = | f (x)| | |
Часть графика функции | |
| Преобразование y = f (| x|) | |
Ось Oy является осью симметрии графика функции y = f (| x|). Часть графика функции | 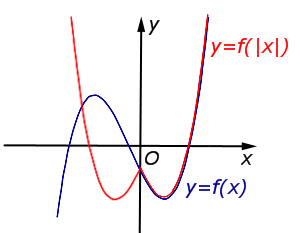 |
Опрацюйте теоритичні відомості
| Преобразование y = f (x + c), где c – число | |
В случае c > 0 график функции y = f (x) переносится влево на расстояние | c | |  |
В случае c < 0 график функции y = f (x) переносится вправо на расстояние | c | |  |
| Преобразование y = f (x) + c, где c – число | |
В случае c > 0 график функции y = f (x) переносится вверх на расстояние | c | |  |
В случае c < 0 график функции y = f (x) переносится вниз на расстояние | c | |  |
| Преобразование y = – f (x) | |
График функции y = f (x) симметрично отражается относительно оси Ox. |  |
| Преобразование y = f ( – x) | |
График функции y = f (x) симметрично отражается относительно оси Oy. |  |
| Преобразование y = f (kx), где k – число | |
В случае k > 1 происходит сжатие графика функции |  |
В случае 0 < k < 1 происходит растяжение графика функции y = f (x) в |  |
В случае – 1 < k < 0 происходит растяжение графика функции y = f (x) в |  |
В случае k < – 1 происходит сжатие графика функции |  |
| Преобразование y = k f (x), где k – число | |
В случае k > 1 происходит растяжение графика функции y = f (x) в k раз от оси Ox. |  |
В случае 0 < k < 1 происходит сжатие графика функции y = f (x) в |  |
В случае – 1 < k < 0 происходит сжатие графика функции y = f (x) в |  |
В случае k < – 1 происходит растяжение графика функции y = f (x) в | k | раз от оси Ox с последующим симметричным отражением графика относительно оси Ox. |  |
| Преобразование y = | f (x)| | |
Часть графика функции | 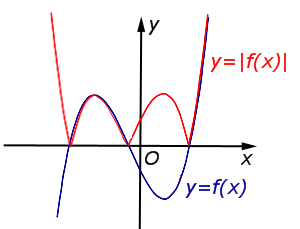 |
| Преобразование y = f (| x|) | |
Ось Oy является осью симметрии графика функции y = f (| x|). Часть графика функции |  |
19.09-24.09 2022
Виконайте завдання
https://vseosvita.ua/test/start/wdk857
12.09-16.09 2022
Подивіться відео урок
https://vseosvita.ua/test/start/iey750
12.09.2022!!!
Увага! Контрольна робота розпочнеться точно за роскладом!
10-Б 12.09 10.00 тривалість 45 хвилин
https://vseosvita.ua/test/start/muo578
10-В 12.09 11.00 тривалість 45 хвилин
https://vseosvita.ua/test/start/txs091
Пройти тестування,відповіді записати у тест,детальні розв'язки завдань надіслати електроною поштою 12.09 до 20.00
Заняття №2 "Нестандартні способи розв'язування квадратних рівнянь"
Перегляньте запис у робочому зошиті
Скористуйтесь теоритичними підказками
Подивіться відео урок
Виконайте завдання
05.09-09.09.2022
Заняття №1 "Повторення.Рівняння"
Завдання: Тест№1
10-Б https://vseosvita.ua/test/start/gmb546
10-В https://vseosvita.ua/test/start/pov403
тест №3 https://vseosvita.ua/test/start/wfj308
26.04-30.04.2021
Онлайн урок відбудеться на платформі Google meet за розкладом.
Примеры решения задач
.png)
.png)
.png)

Примеры решения задач

![]()


Примеры решения задач




Пройдіть тестування https://vseosvita.ua/test/start/wzv203
19.04.2021
Онлайн урок відбудеться на платформі Google meet за розкладом.
Означення
Определение.
Арксинус числа a∈[−1, 1] – это угол −90°≤α≤90° (−π/2≤α≤π/2), синус которого равен a.
Аналогично определяются арккосинус, арктангенс и арккотангенс.
Определение.
Арккосинус числа a∈[−1, 1] – это угол 0°≤α≤180° (0≤α≤π), косинус которого равен a.
Определение.
Арктангенс числа a∈(−∞, +∞) – это угол −90°<α<90° (−π/2<α<π/2), тангенс которого равен a.
Определение.
Арккотангенс числа a∈(−∞, +∞) – это угол 0°<α<180° (0<α<π), котангенс которого равен a.
Формулы перехода от отрицательных значений к положительным:
Функция непрерывна и ограничена на всей своей области определения. Она является строго возрастающей.
- при
- при
- (область определения),
- (область значений).
Функция непрерывна и ограничена на всей своей области определения. Она является строго убывающей и неотрицательной.
- при
- при
- (область определения),
- (область значений).
Корисні посилання
Приклади

Учитывая определения обратных тригонометрических функций получим:

Пройдіть тестування https://vseosvita.ua/test/start/vtv296
12.04.2021
Онлайн урок відбудеться на платформі Google meet за розкладом.
https://vseosvita.ua/test/start/wgj134
Подивіться та виконайте всі завдання за квітень!!!
16.04.2021
Розгляньте приклади побудови графіків
Виконайте практичну роботу:
05.04
Онлайн урок відбудеться на платформі Google meet за розкладом.
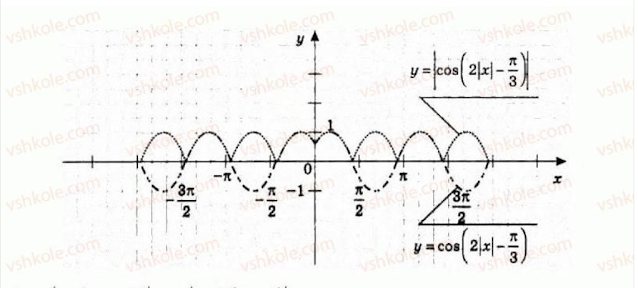
Тригонометричні функції,властивості,графік
Функції y=sin x, y=cos x
Виконай завдання
пройди тестування
09.04
Функції y=tg x, y= ctg x
Тест https://vseosvita.ua/test/start/dmt153
19.03.2021 10-А,Б,В
Тригонометричні функції,властивості,графік
ТЕСТ https://vseosvita.ua/test/start/ntv352
10-Б 09.03
Виконайте завдання у робочих зошитах
1.«Знайди помилку»
1) соs170соs130-sin170sin13°= соs 40;
2) 5соs90° +2соs0° +10соs180° = -8;
3) cos80°sіn100 - sіn800соs10° = sіn 70°;
4) sin ( 3п/2+а) = - sin α
1. tg (π/4-α) і) cos α
2. cos2 α/2 – sin2 α2 п) tg α/2
3. sinα/1+cosα х) sin2α
4. 1+cos2α2 a) cos2α
5. 2sinα cosα г) 1-tgα/1+tgα
6. 2 cos2α – 1 р) sinα
7. 1-cos2α2
Виконайте контрольну роботу на подвійних аркушах
І варіант
Івлєва, Іщук, Кравченко,Личко, Магеррамова, Мевшин, Фуртатов, Шарга, Шкуров, Шмата, Горлатенко, Пархоменко,Шнуровенко
Спростити вираз (1 — 2):
1. 1) sin2 17° + cos2 17°; 2) tg × ctgх; 3) 1 + tg2 4b.
2. 1) 1 ‑ sin2 29°; 2) –sin2 b ‑ cos2 b;
3. Обчислити:
1) sin a, tg a, ctg a, якщо cos a = 0,6 і а єІ ч.
2) cos2 a, якщо tg a = ‑3.
Спростити вираз:
3) tg a ctg a + ctg2 a; 4) (sin b ‑ cos b)2 + 2sin b cos b.
Достатній рівень
1. Спростити вираз (1 – ctg a)2 + (1 + ctg a)2.
2. Довести тотожність ctg2 a ‑ сos2 a = cos2 a ctg2 a.
ІІ-варіант Демідова, Негоіца,Позюченко, Капітонов, Студілко Слободянюк,
Спростити вираз (1 — 2):
1. 1) sin2 71° + cos2 71°; 2) tg × ctgх; 3) 1 + ctg2 3a.
2. 1) 1 ‑ cos2 15°; 2) –3sin2 a ‑ 3cos2 a;
3. Обчислити:
1) cos a, tg a, ctg a, якщо sin a = 0,8 і а є ІІ ч.
2) sin2 a, якщо ctg a = 5.
Спростити вираз:
3) tg2 a + tg a ctg a; 4) (sin x + cos x)2 ‑ 2sin x cos x.
Достатній рівень
1. Спростити вираз (1 + tg a)2 + (1 – tg a)2.
2. Довести тотожність tg2 a ‑ sin2 a = tg2 a sin2 a.
ІІІ-варіант Безух, Біляс, Бондаренко,Даміров, Іщенко, Ткач,
Спростити вираз (1 — 2):
1. 1) соs2 + sin2 ; 2) ctg 1° tg 1°; 3) ctg2 17° + 1.
2. 1) 1 ‑ cos2 28°; 2) –cos2 ‑ sin2 ;
3. Обчислити:
1) sin a, tg a, ctg a, якщо cos a = ‑0,8 і а є ІІ ч. .
2) cos2 b, якщо tg b = 4.
Спростити вираз:
3) 1 ‑ sin a tg a cos a; 4) (1 + ctg b)2 ‑ 2ctg b.
Достатній рівень
1. 1) Обчислити sin a, cos a, tg a, якщо ctg a = ‑ і .
2) Спростити вираз sin2 b + cos4 b(1 + tg2 b).
2. Спростити вираз (sin a + cos a)2 + tg2 a ‑ 2sin a cos a.
Високий рівень
1. Довести тотожність 1 – 3sin2 a cos2 a = sin6 a + cos6 a.
2. tg a + ctg a = 3. Обчислити tg2 a + ctg2 a.
1. 1) sin2 17° + cos2 17°; 2) tg × ctgх; 3) 1 + tg2 4b.
2. 1) 1 ‑ sin2 29°; 2) –sin2 b ‑ cos2 b;
3. Обчислити:
1) sin a, tg a, ctg a, якщо cos a = 0,6 і а єІ ч.
2) cos2 a, якщо tg a = ‑3.
Спростити вираз:
3) tg a ctg a + ctg2 a; 4) (sin b ‑ cos b)2 + 2sin b cos b.
Достатній рівень
1. Спростити вираз (1 – ctg a)2 + (1 + ctg a)2.
2. Довести тотожність ctg2 a ‑ сos2 a = cos2 a ctg2 a.
ІІ-варіант Демідова, Негоіца,Позюченко, Капітонов, Студілко Слободянюк,
Спростити вираз (1 — 2):
1. 1) sin2 71° + cos2 71°; 2) tg × ctgх; 3) 1 + ctg2 3a.
2. 1) 1 ‑ cos2 15°; 2) –3sin2 a ‑ 3cos2 a;
3. Обчислити:
1) cos a, tg a, ctg a, якщо sin a = 0,8 і а є ІІ ч.
2) sin2 a, якщо ctg a = 5.
Спростити вираз:
3) tg2 a + tg a ctg a; 4) (sin x + cos x)2 ‑ 2sin x cos x.
Достатній рівень
1. Спростити вираз (1 + tg a)2 + (1 – tg a)2.
2. Довести тотожність tg2 a ‑ sin2 a = tg2 a sin2 a.
ІІІ-варіант Безух, Біляс, Бондаренко,Даміров, Іщенко, Ткач,
Спростити вираз (1 — 2):
1. 1) соs2 + sin2 ; 2) ctg 1° tg 1°; 3) ctg2 17° + 1.
2. 1) 1 ‑ cos2 28°; 2) –cos2 ‑ sin2 ;
3. Обчислити:
1) sin a, tg a, ctg a, якщо cos a = ‑0,8 і а є ІІ ч. .
2) cos2 b, якщо tg b = 4.
Спростити вираз:
3) 1 ‑ sin a tg a cos a; 4) (1 + ctg b)2 ‑ 2ctg b.
Достатній рівень
1. 1) Обчислити sin a, cos a, tg a, якщо ctg a = ‑ і .
2) Спростити вираз sin2 b + cos4 b(1 + tg2 b).
2. Спростити вираз (sin a + cos a)2 + tg2 a ‑ 2sin a cos a.
Високий рівень
1. Довести тотожність 1 – 3sin2 a cos2 a = sin6 a + cos6 a.
2. tg a + ctg a = 3. Обчислити tg2 a + ctg2 a.
26.02.2021
https://vseosvita.ua/test/start/fgs544
21.01.2021
Тригонометричні функціїї числового аргументу
13.01.2021
Радіанна міра кутів
Онлайн урок відбудеться 14.01 о 09.00 на платформі Google meet.
1. Выразите в радианной мере величины углов
а) 75° и 168°
б)72° и 140°
в)66° и 156°.
2. Выразите в градусной мере величины углов
а) 5π/18 и 17п/36.
б) 11п/12 и 23п/8.
в) 3п/16 и 2 4/9 п.
Відповіді занести у таблицю
|
№ завдання |
відповідь |
відповідь |
відповідь |
|
1 |
|
|
|
|
2 |
|
|
|
Завдання №2
1.Угол 150° равен:
![]()
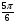
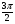
![]()
2.Сравнить ![]()
> < = нет верного ответа
Перед выполнением заданий 3 и 5 внимательно посмотрите видео урок №1
3.Радиус окружности равен 2 см. 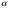 =150°.Найти длину дуги см:
=150°.Найти длину дуги см:
4.Выберите верный ответ. Угол 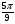 равен:
равен:
30° 100° 50° Нет верного ответа
5.Дуга длиной 0,49м стягивает центральный угол 0,7 рад. Радиус окружности равен:
0,7 м 7 см. 0,3м 0,07 м.
Відповіді занести у таблицю
|
№ завдання |
відповідь |
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
Відповіді (розв язок + таблиця)надіслати електронною поштою до 17.01
:
20.11.2020
https://vseosvita.ua/test/start/vnf537
10.11.2020
Онлайн урок відбудеться 10.11 о 09.00 на платформі Google meet.
Тест №3 https://vseosvita.ua/test/start/zfn363
03.11.2020
Онлайн урок відбудеться 10.11 о 09.00 на платформі Google meet.
Тест №2 https://vseosvita.ua/test/start/svw525
Вивчаємо нову тему!
23.10.2020 10А,Б,В
21.05.2020
Тест "Нерівності"
https://forms.gle/jWUVmrC8DNo9ZvSz7
Термін виконання до 24.05
Розв'язки завдань №4 і №7 надіслати електронною поштою.
18.05.2020
Любі мої, нагадую,що до закінчення навчального року залишилося 10 днів!
Оцінки за дистанційне навчання враховуються у семестрову оцінку.
Продовжуємо повторення!

15.05.2020
11.05.2020
04.05.2020
оцінки на платформі дистанційного навчання тисни тут
Будьте щасливі та здорові.
Модуль:
Параметр:
Готуємося до контрольної роботи!!!
28.04.2020
Тесты открыты до 20.00
27.04.2020
Передивіться відео урок :" Рівняння з параметром"і тільки потім виконуйте вправи!
25.04.2020
Нагадую! Всі тести будуть знову відкриті 28.04 з 9.00 до 19.00
21.04 2020
Уважно перегляньте відео урок з розв язування рівнянь з параметрами!
Завдання№2
(а^2 а- во 2 степеню , / дріб)
ах - 3х = 4( х+ 1 )
а / (х+3) + 3 / ( х+2 )= а^2 + 2а / (х+2)(х+3)
18.04.2020
А тепер про приємне:
Вітаю всіх з Великоднем! Щастя, терпіння, здійснення мрій!
17.04.2020
Всі тести відкриті до 18.04 до 20.00
Після цього будуть підбиті підсумки.Більше до цих завдань повертатися не будемо!!!
16.04.2020
а) І х І - І х-2 І=2
б)І 7х - 12 І - І 7х - 11 І =1
в)І х - 1 І - 2 І х + 3 І = х + 7
15.04.2020
"Доброго дня. Гарного настрою"...
а) І х І - І х-2 І=2
б) І 7х - 12 І - І 7х - 11 І =1
в) І х - 1 І - 2 І х + 3 І = х + 7
в) І х - 1 І - 2 І х + 3 І = х + 7
Виконайте тест №5
14.04.2020
В. Г. :" Доброго дня , гарного настрою"...Будьте щасливі та здорові. 💖
оцінки на платформі дистанційного навчання тисни тут
13.04.2020
В. Г. :" Доброго дня , гарного настрою"...
Передивіться відео урок :" Рівняння з модулем". Ті, хто вже виконав тест №4 допустили багато помилок. ще раз прошу - передивіться відео.
У зошиті розв язати та надіслати електронною наступні завдання:
Виконайте тест №5
Тест №5
https://forms.gle/AQnXhmphY458r8feA
Завдання виконати до 18.04.2020!
10.04.2020
З любов ю ваша Шеремет В.Г.
09.04.2020
Будьте уважними. Бажаю наснаги у навчанні.
Рівняння з модулем
07.04.2020
Відповіді до тестів №1-№3 з 11.04.2020 прийматися не будуть
06.04.2020
Після перегляду виконайте завдання №3 за посиланням.
Тест №3 https://forms.gle/zur4eSrxyCFgRgKt7
термін до 10.04.2020
ТРИГОНОМЕТРИЧНІ РІВНЯННЯ ЯКІ ЗВОДЯТЬСЯ ДО КВАДРАТНИХ
Однорідні тригонометричні рівняння
Рівняння що розкладаються на множники
29.03.2020
Пропоную вам трохи розважитися
Пропоную вам трохи розважитися
https://learningapps.org/5598796
https://learningapps.org/5379459
https://learningapps.org/5561761
https://learningapps.org/1728866
https://learningapps.org/648243
https://learningapps.org/368638
https://learningapps.org/6996562
https://learningapps.org/2464559
https://learningapps.org/2071040
https://learningapps.org/6994768
https://learningapps.org/5149861
26.03.2020
Любі діти прошу вас відповідально ставитися до завдань,які пропонують вам вчителі.
Виконайте завдання контрольної роботи .Відповіді можна надіслати за посиланням, або на електронну пошту. Оцінку повідомлю у групі.
Термін виконання: 10.04.2020
ДЛЯ СПРОЩЕННЯ ПРАВОЇ ЧАСТИНИ РІВНЯНЬ ВИКОРИСТАЙТЕ ТРИГОНОМЕТРИЧНІ ФОРМУЛИ ПОДВІЙНОГО КУТА, формули суми ,ТАБЛИЦЮ ЗНАЧЕНЬ ДЛЯ ДЕЯКИХ КУТІВ.
Рівняння Sin x+cos x=0- однорідне. треба ділити на COS X
1. Розв’яжіть рівняння:
2sinx-1=0
2. Розв’яжіть рівняння:
sin2 x-1=cos2 x
3. Розв’яжіть рівняння:
tg 0,5х +1=0
4.Розв’яжіть рівняння:
4sin2 x-sin2x=0
5. Розв’яжіть рівняння:
cos5x-cos3x=0
6. Розв’яжіть рівняння:
cos3x+2cosx=0 *2cosx = cosx+ cosx
Рівняння SIN X+COS X=0- ОДНОРІДНЕ. ТРЕБА ДІЛИТИ НА COS X
https://forms.gle/GpgsLVmdcNk65SBG7 відповіді можна надіслати за посиланнямВаріант 2
1. Розв’яжіть рівняння:
4cosx-1=3
2. Розв’яжіть рівняння:
cos2 x=sinx+1
3. Розв’яжіть рівняння:
ctg2x>√3
4. Розв’яжіть рівняння:
cos2x-2cos2x+1=0
5. Розв’яжіть рівняння:
cos3x+cosx-4cos2x=0
6. Розв’яжіть рівняння:
sin3x-2sinx=0 * 2sinx= sinx+ sinx










































































































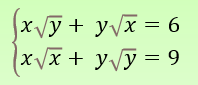























































































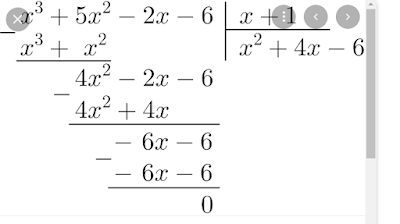






















![D(\arcsin x)=[-1;1]\qquad](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd3f4bf3e28749594b902927c25d875de43acb55)
![E(\arcsin x)=\left[-{\frac {\pi }{2}};{\frac {\pi }{2}}\right]\qquad](https://wikimedia.org/api/rest_v1/media/math/render/svg/35cf0029d59f77e2edbf4e49629cd8563aa42d0b)




![{\displaystyle D(\arccos x)=[-1;1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9ef5f8e6b88d4178d2c26e775ab701640e82225)
![{\displaystyle E(\arccos x)=[0;\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d072482a273c2e42cde2fd1e031be84c87bec721)










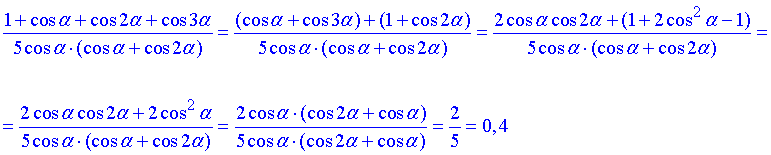
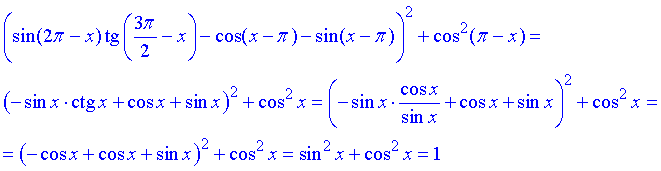









Комментариев нет:
Отправить комментарий