Виконуйте завдання
Після проходження тесту відправити наелектронну пошту фото звіт
Тестування:https://vseosvita.ua/test/start/vwo083
Рівняння,
що містить невідоме лише в показнику степеня, називається показниковим. Існує
декілька типів показникових рівнянь:
1.
Найпростіші та які зводяться до них;
2.
Показникові рівняння які зводяться до
алгебраїчних;
3.
Нестандартні показникові рівняння.
Показникове рівняння – це рівняння, у яких змінна
знаходиться в показнику степеня, найпростіше з них ах = b , а
> 0, а ≠ 1. (Слайд 8)
І. Найпростіші
показникові рівняння та ті, що зводяться до них шляхом:
·
зведення до однієї основи;
·
винесення
спільного множника за дужки;
|
|
Алгоритм |
|
|
1.
Винести
за дужки спільний множник. 2.
Виконати
дії в дужках. 3.
На вираз
у дужках поділити ліву і праву частину рівняння. 4.
Звести
рівняння до однієї основи. 5.
Прирівняти
показники. 6. Записати відповідь. |
·
ділення обох
частин на степінь
|
|
Алгоритм |
|
|
1. Поділити
обидві частини рівняння на один із степенів. 2. Звести
обидві частини рівняння до однієї основи. 3. Прирівняти
показники. 4. Розв’язати
одержане рівняння 5. Записати
відповідь |
ІІ. Показникові рівняння які зводяться до алгебраїчних:
·
Зведенням до
квадратних шляхом заміни змінної;
|
|
Алгоритм |
|
|
1. Звести
степені до однакової основи. 2. Виконати
заміну. 3. Розв’язати
одержане квадратне рівняння відносно нової
заміни. 4. Повернутися
до заміни і розв’язати відповідне показникові
рівняння. 5. Записати
відповідь. |
· Однорідні
|
|
Алгоритм розв’язання |
|
|
1. Оскільки
, тому
можна поділити обидві частини
рівняння на . 2. Виконати
заміну. 3. Розв’язати
одержане квадратне рівняння
відносно нової заміни. 4. Повернутися
до заміни і розв’язати відповідне
показникові рівняння. 5. Записати
відповідь. |
ІІІ.
Нестандартні показникові рівняння для розв’язку яких, використовують різні
прийоми.
Завдання: відповіді записувати десятковими дробами

№2 Тестування https://vseosvita.ua/test/start/yie618
Час тестування 15 хвилин
. Властивості степеня дійсного числа з дійсним показником
1) ![]() ; 2)
; 2) 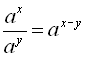 ;
;
3) ![]() ; 4)
; 4) ![]() ;
;
5) 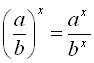 ; 6)
; 6) 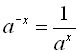 ;
;
7) ![]() ; 8)
; 8) ![]() ;
;
9) ![]() .
.
Приклади
1. Записати вираз у вигляді степеня 
Розв’язання
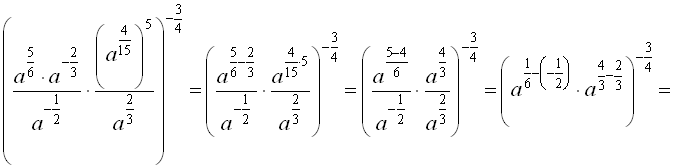
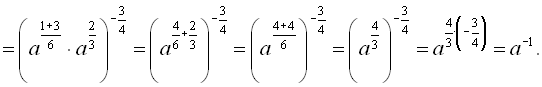
Відповідь: ![]() .
.
2. Обчислити 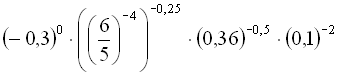 .
.
Розв’язання
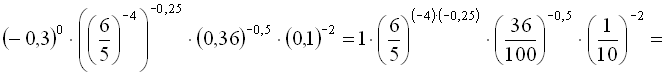
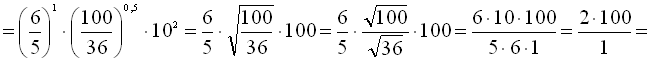
![]()
Відповідь: 200.
Рівняння називається тригонометричним, якщо невідома величина знаходиться під знаком тригонометричних функцій. Найпростішими тригонометричними рівняннями називаються рівняння 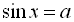 ,
, 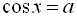 ,
, 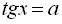 ,
, 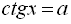 . Розв’язати найпростіше тригонометричне рівняння – означає знайти множину всіх кутів, що мають дане значення
. Розв’язати найпростіше тригонометричне рівняння – означає знайти множину всіх кутів, що мають дане значення 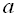 тригонометричної функції. Якщо тригонометричне рівняння не є найпростішим, то за допомогою тотожних перетворень його треба звести до одного або кількох найпростіших, розв’язання яких визначається стандартними формулами.
тригонометричної функції. Якщо тригонометричне рівняння не є найпростішим, то за допомогою тотожних перетворень його треба звести до одного або кількох найпростіших, розв’язання яких визначається стандартними формулами.
При використанні формул для розв’язування тригонометричних рівнянь враховуйте, що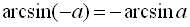 ;
; 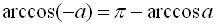 ;
;
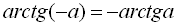 ;
; 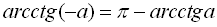 .
.
Прередивіться відео уроки
1.Найпростіші рівняння
2.Квадратні та такі,що зводяться до квадратних
Рівняння називається тригонометричним, якщо невідома величина знаходиться під знаком тригонометричних функцій. Найпростішими тригонометричними рівняннями називаються рівняння ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Розв’язати найпростіше тригонометричне рівняння – означає знайти множину всіх кутів, що мають дане значення
. Розв’язати найпростіше тригонометричне рівняння – означає знайти множину всіх кутів, що мають дане значення ![]() тригонометричної функції. Якщо тригонометричне рівняння не є найпростішим, то за допомогою тотожних перетворень його треба звести до одного або кількох найпростіших, розв’язання яких визначається стандартними формулами.
тригонометричної функції. Якщо тригонометричне рівняння не є найпростішим, то за допомогою тотожних перетворень його треба звести до одного або кількох найпростіших, розв’язання яких визначається стандартними формулами.
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Прередивіться відео уроки
1.Найпростіші рівняння
2.Квадратні та такі,що зводяться до квадратних
Способи розв'язування тригонометричних рівнянь
1) Заміна змінних при розв’язуванні тригонометричних рівнянь
Сьогодні ми навчимось розв’язувати складніші тригонометричні рівняння, які шляхом поточних перетворень можна звести до рівнянь з однією тригонометричною функцією, потім зробити заміну і звести до алгебраїчного рівняння.
Приклад 1. Розв’язати рівняння
2 sin2x + sinx – 1 = 0
В ході пояснення задаю питання учням, спонукаю до спільного обговорення розв’язку, учні записують розв’язання у зошит.
Розв’язання.
Введемо нову змінну t = sin x.
Оскільки sin x – функція обмежена, то t ϵ [-1;1]
Тоді дане рівняння буде мати вигляд 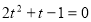 .
.
Розв’яжемо його: 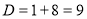 ,
, 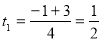 ,
, 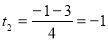 .
.
Тому, 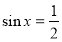 або
або 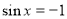 .
.
1) 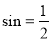 ,
,
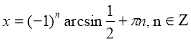 ,
,
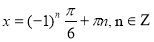 .
.
2) 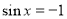 ,
,
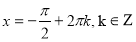 .
.
Відповідь: 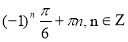 ,
, 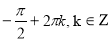 .
.
2) Розв’язування тригонометричних рівнянь зведенням до однієї функції (з однаковим аргументом).
Приклад 2. Розв’язати рівняння
6sin2x + 5cosx – 2 = 0
Обговорюється хід розв’язування рівняння, проектується розв’язання, записують у зошит.
Замінимо  на
на 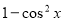 і отримаємо квадратне рівняння відносно
і отримаємо квадратне рівняння відносно 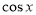 .
.
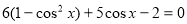 ,
,
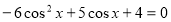 ,
,
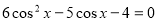 .
.
Нехай 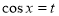 ,
, 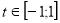 , тоді
, тоді 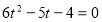 ,
, 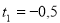 ,
, 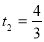 - сторонній корінь. Отже,
- сторонній корінь. Отже, 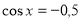 ,
,
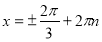 ,
, 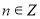 .
.
Відповідь: 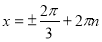 ,
, 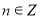 .
.
Алгоритм розв’язування рівнянь зведенням до однієї функції (з однаковим аргументом).
- Спробувати всі тригонометричні функції звести до одного аргументу.
- Якщо вдалося звести до одного аргументу, то спробувати всі тригонометричні вирази звести до однієї функції.
- Зробити заміну.
- Звести рівняння до квадратного.
- Розв’язати квадратне рівняння.
- Повернутись до заміни і розв’язати утворені рівняння.
- Записати відповідь.
Приклад 3. Розв’язати рівняння 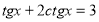
Чи можна це рівняння записати відносно однієї тригонометричної функції? Виконайте це.
Чи можна це рівняння записати у вигляді квадратного рівняння відносно однієї змінної?
Розв’яжіть рівняння, перевірте правильність виконання, виправте помилки.
Розв’язання. Оскільки 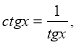 то рівняння можна записати у вигляді
то рівняння можна записати у вигляді
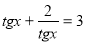 .
.
Позначимо 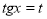 . Отримаємо рівняння
. Отримаємо рівняння 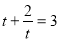 , яке зводиться до квадратного
, яке зводиться до квадратного
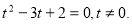
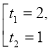
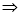
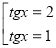
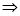
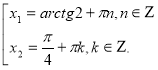
Відповідь: 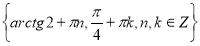 .
.
3) Розв’язання тригонометричних рівнянь за допомогою розкладання на множники.
Приклад 4. Розв’язати рівняння 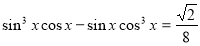 .
.
Розв'язання. У лівій частині рівняння винесемо за дужки спільний множник і застосуємо формули подвійного кута:  ,
,
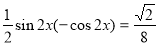 ,
,
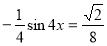 ,
,
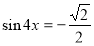 ,
,
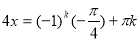 ,
, 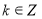 ;
;
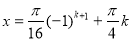 ,
, 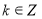 .
.
Відповідь: 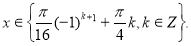
4) Однорідні тригонометричні рівняння.
Якщо всі члени рівняння у лівій і правій частинах якого стоять многочлени від двох змінних (або від двох функцій однієї змінної) мають однаковий сумарний степінь, то рівняння називається однорідним. Розв’язують однорідне рівняння діленням на найвищий степінь однієї змінної.
Зауваження. Дотримуючись цього орієнтира, доводиться ділити обидві частини рівняння на вираз зі змінною. При цьому можлива втрата коренів, якщо коренями є числа, при яких дільник дорівнює нулю. Щоб уникнути втрати коренів, необхідно окремо розглянути випадок, коли вираз, на який ми збираємось ділити обидві частини рівняння, дорівнював нулю, і лише після цього виконувати ділення на вираз що не дорівнює нулю.
Розглянемо рівняння виду 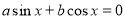 (однорідне рівняння 1-го степеня), де а і b не дорівнюють нулю. Значення х, при яких cos x дорівнює нулю, не задовольняє даному рівнянню, бо тоді і sin x теж дорівнював би нулю, а cos x і sin x не можуть одночасно дорівнювати нулю. Тому можна розділити обидві частини рівняння почленно на cos x. Маємо:
(однорідне рівняння 1-го степеня), де а і b не дорівнюють нулю. Значення х, при яких cos x дорівнює нулю, не задовольняє даному рівнянню, бо тоді і sin x теж дорівнював би нулю, а cos x і sin x не можуть одночасно дорівнювати нулю. Тому можна розділити обидві частини рівняння почленно на cos x. Маємо: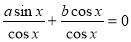 ,
, 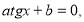
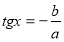 .
.
Розв’язавши дане тригонометричне рівняння отримуємо корені.
Рівняння виду
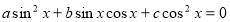
називається однорідним рівнянням 2-го степеня.
Якщо числа a, b, c не дорівнюють нулю, то розділимо дане рівняння на 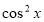 (або на
(або на 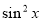 ). (У даному рівнянні
). (У даному рівнянні 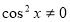 , бо в супротивному випадку
, бо в супротивному випадку 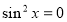 , а cos x і sin x не можуть одночасно дорівнювати нулю). Тоді
, а cos x і sin x не можуть одночасно дорівнювати нулю). Тоді
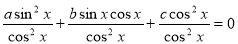
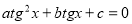 .
.
Розв'язавши отримане, рівняння одержимо корені даного рівняння.
Приклад 5. Розв’язати на дошці, коментуючи кожен крок. Залучати студентів до обговорення.
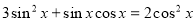
ОДЗ: 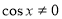
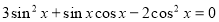 ділимо на
ділимо на 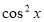
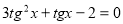
Заміна 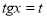 ,
, 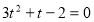 ,
, 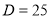 ,
, 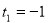 ,
, 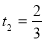 .
.
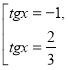
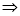

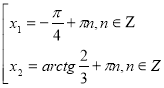
Відповідь: 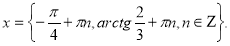
5. Метод введення допоміжного кута.
Розглянемо рівняння виду asinx + bcosx = c. Очевидно, що 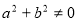 .
.
Поділимо обидві частини рівняння на 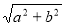 і покладемо
і покладемо 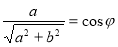 та
та 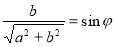 , маємо рівняння
, маємо рівняння 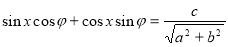 , або
, або 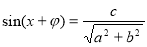 . Отже, дістали просте тригонометричне рівняння яке має розв’язки за умови
. Отже, дістали просте тригонометричне рівняння яке має розв’язки за умови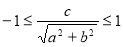 .
.
Виконуємо завдання
11.09.23 Домашне завдання :
Вибрати та розв'язати будь які чотири рівняння
Способи розв'язування тригонометричних рівнянь
1) Заміна змінних при розв’язуванні тригонометричних рівнянь
Сьогодні ми навчимось розв’язувати складніші тригонометричні рівняння, які шляхом поточних перетворень можна звести до рівнянь з однією тригонометричною функцією, потім зробити заміну і звести до алгебраїчного рівняння.
Приклад 1. Розв’язати рівняння
2 sin2x + sinx – 1 = 0
В ході пояснення задаю питання учням, спонукаю до спільного обговорення розв’язку, учні записують розв’язання у зошит.
Розв’язання.
Введемо нову змінну t = sin x.
Оскільки sin x – функція обмежена, то t ϵ [-1;1]
Тоді дане рівняння буде мати вигляд ![]() .
.
Розв’яжемо його: ![]() ,
, ![]() ,
, ![]() .
.
Тому, ![]() або
або ![]() .
.
1) ![]() ,
,
![]() ,
,
![]() .
.
2) ![]() ,
,
![]() .
.
Відповідь: ![]() ,
, ![]() .
.
2) Розв’язування тригонометричних рівнянь зведенням до однієї функції (з однаковим аргументом).
Приклад 2. Розв’язати рівняння
6sin2x + 5cosx – 2 = 0
Обговорюється хід розв’язування рівняння, проектується розв’язання, записують у зошит.
Замінимо ![]() на
на ![]() і отримаємо квадратне рівняння відносно
і отримаємо квадратне рівняння відносно ![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
Нехай ![]() ,
, ![]() , тоді
, тоді ![]() ,
, ![]() ,
, ![]() - сторонній корінь. Отже,
- сторонній корінь. Отже, ![]() ,
,
![]() ,
, ![]() .
.
Відповідь: ![]() ,
, ![]() .
.
Алгоритм розв’язування рівнянь зведенням до однієї функції (з однаковим аргументом).
- Спробувати всі тригонометричні функції звести до одного аргументу.
- Якщо вдалося звести до одного аргументу, то спробувати всі тригонометричні вирази звести до однієї функції.
- Зробити заміну.
- Звести рівняння до квадратного.
- Розв’язати квадратне рівняння.
- Повернутись до заміни і розв’язати утворені рівняння.
- Записати відповідь.
Приклад 3. Розв’язати рівняння ![]()
Чи можна це рівняння записати відносно однієї тригонометричної функції? Виконайте це.
Чи можна це рівняння записати у вигляді квадратного рівняння відносно однієї змінної?
Розв’яжіть рівняння, перевірте правильність виконання, виправте помилки.
Розв’язання. Оскільки ![]() то рівняння можна записати у вигляді
то рівняння можна записати у вигляді
![]() .
.
Позначимо ![]() . Отримаємо рівняння
. Отримаємо рівняння ![]() , яке зводиться до квадратного
, яке зводиться до квадратного![]()
![]()
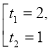
![]()
![]()
![]()
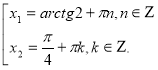
Відповідь: ![]() .
.
3) Розв’язання тригонометричних рівнянь за допомогою розкладання на множники.
Приклад 4. Розв’язати рівняння ![]() .
.
Розв'язання. У лівій частині рівняння винесемо за дужки спільний множник і застосуємо формули подвійного кута: ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
, ![]() ;
;
![]() ,
, ![]() .
.
Відповідь: ![]()
4) Однорідні тригонометричні рівняння.
Якщо всі члени рівняння у лівій і правій частинах якого стоять многочлени від двох змінних (або від двох функцій однієї змінної) мають однаковий сумарний степінь, то рівняння називається однорідним. Розв’язують однорідне рівняння діленням на найвищий степінь однієї змінної.
Зауваження. Дотримуючись цього орієнтира, доводиться ділити обидві частини рівняння на вираз зі змінною. При цьому можлива втрата коренів, якщо коренями є числа, при яких дільник дорівнює нулю. Щоб уникнути втрати коренів, необхідно окремо розглянути випадок, коли вираз, на який ми збираємось ділити обидві частини рівняння, дорівнював нулю, і лише після цього виконувати ділення на вираз що не дорівнює нулю.
Розглянемо рівняння виду ![]() (однорідне рівняння 1-го степеня), де а і b не дорівнюють нулю. Значення х, при яких cos x дорівнює нулю, не задовольняє даному рівнянню, бо тоді і sin x теж дорівнював би нулю, а cos x і sin x не можуть одночасно дорівнювати нулю. Тому можна розділити обидві частини рівняння почленно на cos x. Маємо:
(однорідне рівняння 1-го степеня), де а і b не дорівнюють нулю. Значення х, при яких cos x дорівнює нулю, не задовольняє даному рівнянню, бо тоді і sin x теж дорівнював би нулю, а cos x і sin x не можуть одночасно дорівнювати нулю. Тому можна розділити обидві частини рівняння почленно на cos x. Маємо:![]() ,
, ![]()
![]() .
.
Розв’язавши дане тригонометричне рівняння отримуємо корені.
Рівняння виду
![]()
називається однорідним рівнянням 2-го степеня.
Якщо числа a, b, c не дорівнюють нулю, то розділимо дане рівняння на ![]() (або на
(або на ![]() ). (У даному рівнянні
). (У даному рівнянні ![]() , бо в супротивному випадку
, бо в супротивному випадку ![]() , а cos x і sin x не можуть одночасно дорівнювати нулю). Тоді
, а cos x і sin x не можуть одночасно дорівнювати нулю). Тоді
![]()
![]() .
.
Розв'язавши отримане, рівняння одержимо корені даного рівняння.
Приклад 5. Розв’язати на дошці, коментуючи кожен крок. Залучати студентів до обговорення.
![]()
ОДЗ: ![]()
![]() ділимо на
ділимо на ![]()
![]()
Заміна ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
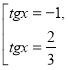
![]()
![]()
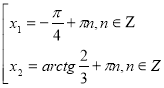
Відповідь: ![]()
5. Метод введення допоміжного кута.
Розглянемо рівняння виду asinx + bcosx = c. Очевидно, що ![]() .
.
Поділимо обидві частини рівняння на ![]() і покладемо
і покладемо ![]() та
та ![]() , маємо рівняння
, маємо рівняння ![]() , або
, або ![]() . Отже, дістали просте тригонометричне рівняння яке має розв’язки за умови
. Отже, дістали просте тригонометричне рівняння яке має розв’язки за умови![]() .
.
Виконуємо завдання
11.09.23 Домашне завдання :
13.09.23
Ірраціональні ріняння та нерівності
Теоритичні відомості Рівняння
13.09.23
Ірраціональні ріняння та нерівності
Ірраціональними називаються рівняння, у якиx змінна міститься під знаком кореня (радикала) або під знаком піднесення до дробового степеня.
В окремих випадках, не розв’язуючи дане ірраціональне рівняння, можна встановити, що воно не має коренів. Наприклад, рівняння 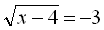 не має коренів, бо арифметичний корінь не може бути від’ємним.
не має коренів, бо арифметичний корінь не може бути від’ємним.
Рівняння 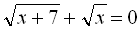 не має розв’язків, бо обидва доданки є арифметичними коренями, а тому не можуть бути від’ємними. А сума двох невід’ємних чисел дорівнює нулю лише тоді, коли кожен доданок дорівнює нулю. Одночасно ж вирази
не має розв’язків, бо обидва доданки є арифметичними коренями, а тому не можуть бути від’ємними. А сума двох невід’ємних чисел дорівнює нулю лише тоді, коли кожен доданок дорівнює нулю. Одночасно ж вирази 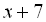 і
і 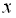 нулю дорівнювати не можуть.
нулю дорівнювати не можуть.
Основними методами розв’язування ірраціональних рівнянь є метод піднесення обох частин рівняння до одного і того самого степеня та метод введення нових змінних.
При розв’язуванні ірраціональних рівнянь методом піднесення обох частин до парного степеня можуть з’явитися побічні корені. Це відбувається за рахунок того, що при піднесенні обох частин початкового рівняння 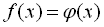 до парного степеня дістаємо рівняння, що є результатом не тільки рівняння
до парного степеня дістаємо рівняння, що є результатом не тільки рівняння 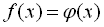 , але і рівняння
, але і рівняння 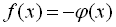 , оскільки і
, оскільки і 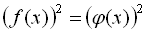 , і
, і 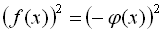 . Так, наприклад, візьмемо рівняння
. Так, наприклад, візьмемо рівняння 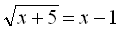 . Піднісши обидві частини цього рівняння до квад-рата, дістанемо
. Піднісши обидві частини цього рівняння до квад-рата, дістанемо 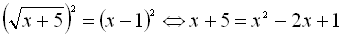
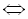
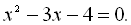 Коренями цього рівняння є числа
Коренями цього рівняння є числа 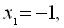
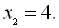 Однак після перевірки переконуємось, що
Однак після перевірки переконуємось, що 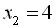 є коренем рівняння
є коренем рівняння 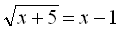 , а
, а 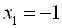 є побічним коренем.
є побічним коренем.
Приступаючи до розв’язання ірраціонального рівняння, що містить парні степені радикалів, буває корисним знаходження області допустимих значень (ОДЗ), це, як правило, полегшує розв’язування рівняння. Якщо робити лише еквівалентні перетворення, то перевірку робити не потрібно.
Розглянемо рівняння виду 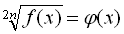 . Очевидно, що ліва частина рівняння, яка містить радикал парного степеня, не може бути від’ємна, а отже невід’ємна і права частина даного рівняння. Враховуючи область допустимих значень, підкореневий вираз також не може бути від’ємним. Отже, рівняння виду
. Очевидно, що ліва частина рівняння, яка містить радикал парного степеня, не може бути від’ємна, а отже невід’ємна і права частина даного рівняння. Враховуючи область допустимих значень, підкореневий вираз також не може бути від’ємним. Отже, рівняння виду 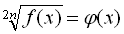 рівносильне такій системі:
рівносильне такій системі:
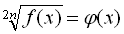
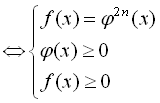 .
.
У системі Maple ірраціональні рівняння, як і раціональні, розв’язу-ються за допомогою функції solve(). Для позначення кореня використовуємо функцію sqrt ().
Приклад 1. Розв’язати рівняння 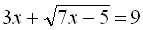 .
.
Розв’язання
Дане рівняння можна звести до вигляду 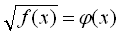 , тобто
, тобто 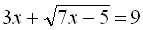
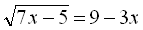
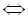
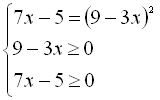
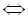
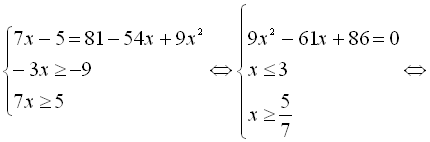
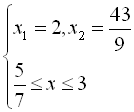 .
.
З даної системи випливає, що лише 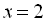 є коренем початкового рівняння.
є коренем початкового рівняння.
Розв’язання рівняння виду 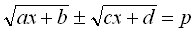 , де
, де 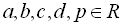 , здійснюється піднесенням обох частин рівняння до квадрату, «ізолюванням» радикала, який при цьому отримується, і повторним піднесенням обох частин рівняння до квадрата. В результаті таких перетворень рівняння даного виду зводиться до раціонального.
, здійснюється піднесенням обох частин рівняння до квадрату, «ізолюванням» радикала, який при цьому отримується, і повторним піднесенням обох частин рівняння до квадрата. В результаті таких перетворень рівняння даного виду зводиться до раціонального.
Приклад 2. Розв’язати рівняння 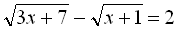 .
.
Розв’язання
Область визначення даного рівняння визначається в результаті розв’-
язання системи нерівностей 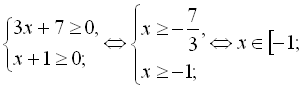
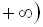 .
.
Перетворимо дане рівняння:
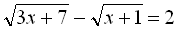
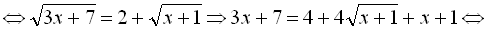
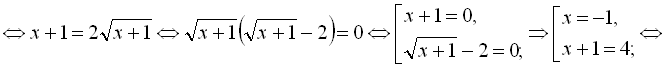
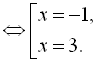
Обидва знайдені корені належать ОДЗ.
Відповідь: 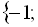
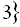 .
.
Приклад 3. Розв’язати рівняння 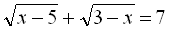 .
.
Розв’язання
Знайдемо для початку область допустимих значень: 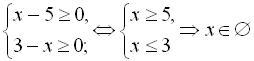 .
.
Оскільки область допустимих значень виявилась пустою множиною, то і розв’язків дане рівняння не має.
Відповідь: 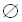 .
.
Приклад 4. Розв’язати рівняння 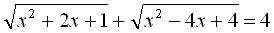 .
.
Розв’язання
Обидва підкореневі вирази є повними квадратами, тому
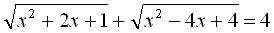
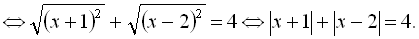
Тобто дане ірраціональне рівняння звелося до раціонального рівняння з двома модулями.
Приклад розв’язання рівняння такого типу наводився раніше.
Відповідь: 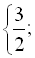
 .
.
Рівняння виду 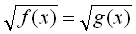 можна розписати за допомогою змішаних систем:
можна розписати за допомогою змішаних систем:
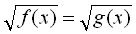
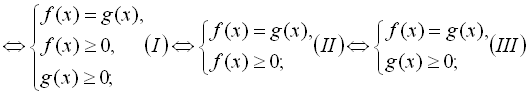
З наведених вище трьох систем вибирають звичайно ту, де простіше розв’язати нерівність (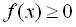 або
або 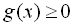 ). Якщо ж обидві нерівності
). Якщо ж обидві нерівності 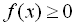 і
і 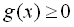 розв’язати нескладно, то можна вибрати першу систему, яка хоча і містить одну зайву нерівність, є більш наочною, ніж ІІ і ІІІ.
розв’язати нескладно, то можна вибрати першу систему, яка хоча і містить одну зайву нерівність, є більш наочною, ніж ІІ і ІІІ.
Приклад 5. Розв’язати рівняння 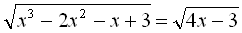 .
.
Розв’язання
Для розв’язання даного рівняння обираємо ІІІ систему:
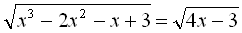
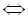
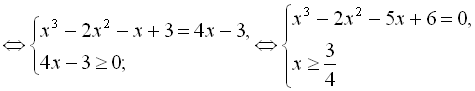 .
.
Окремо розв’яжемо рівняння 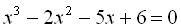 нашої системи. Методом підбору знаходимо цілий корінь даного рівняння. Для цього виписуємо дільники вільного члена: ±1; ±2; ±3. При підборі знаходимо, що коренями є -2; 1; 3. Тоді
нашої системи. Методом підбору знаходимо цілий корінь даного рівняння. Для цього виписуємо дільники вільного члена: ±1; ±2; ±3. При підборі знаходимо, що коренями є -2; 1; 3. Тоді 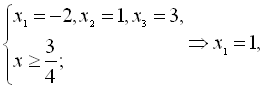
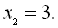
Відповідь: 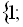
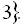
3),x=-2);
Приклад 6. Розв’язати рівняння 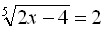 .
.
Розв’язання
Піднесемо обидві частини початкового рівняння до п’ятого степеня, дістанемо: 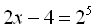 , звідки
, звідки 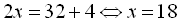 .
.
Перевірка: Підставивши 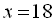 в початкове рівняння, дістанемо
в початкове рівняння, дістанемо 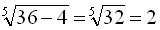 , тобто
, тобто 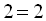 – правильна рівність
– правильна рівність 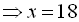 є коренем.
є коренем.
Відповідь: 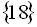 .
.
Приклад 7. Розв’язати рівняння 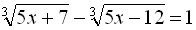 .
.
Розв’язання
ОДЗ початкового рівняння – всі дійсні числа. Піднесемо обидві частини рівняння до кубу:
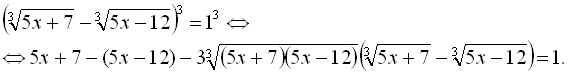
Замінимо різницю 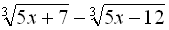 правою частиною первинного рівняння, тобто 1:
правою частиною первинного рівняння, тобто 1: 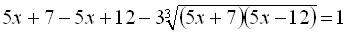 .
.
Ізолюємо кубічний корінь, що залишився, і піднесемо обидві частини рівняння до кубу: 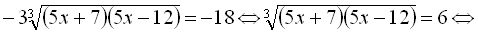
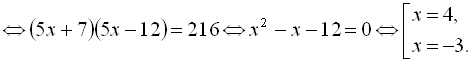
Виконавши перевірку, знайдемо, що множиною розв’язків даного рівняння є 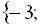
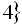 .
.
Відповідь: 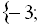
 .
.
НерівностіСпособи розв'язання ірраціональних нерівностей:
- Розв’язування найпростіших ірраціональних нерівностей.
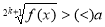
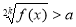
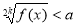
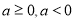
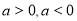
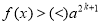
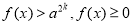
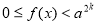 , розв’язків немає
, розв’язків немає
Приклад 1. Розв’яжіть нерівність 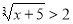 .
.
Розв’язання. Задана нерівність рівносильна нерівності 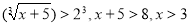 .
.
Відповідь: 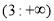 .
.
- Спосіб рівносильних перетворень:
-
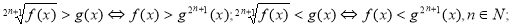
-
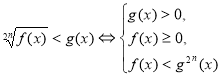 .
.
Приклад 2. Розв’яжіть нерівність 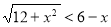 .
.
Розв’язання. Нерівність рівносильна системі нерівностей:
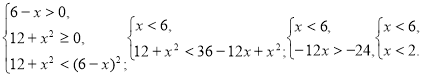
Відповідь: 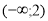 .
.
-

Приклад 3. Розв’яжіть нерівність 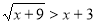 .
.
Розв’язання. Нерівність рівносильна сукупності нерівностей
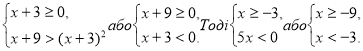
Відповідь: 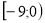 .
.
- Метод інтервалів.
Приклад 4. Розв’яжіть нерівність  .
.
Розв’язання. ОДЗ нерівності 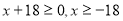 . Задана нерівність рівносильна нерівності
. Задана нерівність рівносильна нерівності 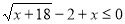 . Позначимо
. Позначимо 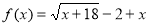 . Нулі функції
. Нулі функції 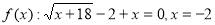 . На області визначення функції позначимо її нулі й на здобутих проміжках визначимо знаки функції:
. На області визначення функції позначимо її нулі й на здобутих проміжках визначимо знаки функції:

Відповідь: 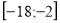 .
.
Виконуемо завдання
Тестуванняhttps://vseosvita.ua/test/start/npd124 8б
Ірраціональними називаються рівняння, у якиx змінна міститься під знаком кореня (радикала) або під знаком піднесення до дробового степеня.
В окремих випадках, не розв’язуючи дане ірраціональне рівняння, можна встановити, що воно не має коренів. Наприклад, рівняння ![]() не має коренів, бо арифметичний корінь не може бути від’ємним.
не має коренів, бо арифметичний корінь не може бути від’ємним.
Рівняння ![]() не має розв’язків, бо обидва доданки є арифметичними коренями, а тому не можуть бути від’ємними. А сума двох невід’ємних чисел дорівнює нулю лише тоді, коли кожен доданок дорівнює нулю. Одночасно ж вирази
не має розв’язків, бо обидва доданки є арифметичними коренями, а тому не можуть бути від’ємними. А сума двох невід’ємних чисел дорівнює нулю лише тоді, коли кожен доданок дорівнює нулю. Одночасно ж вирази ![]() і
і ![]() нулю дорівнювати не можуть.
нулю дорівнювати не можуть.
Основними методами розв’язування ірраціональних рівнянь є метод піднесення обох частин рівняння до одного і того самого степеня та метод введення нових змінних.
При розв’язуванні ірраціональних рівнянь методом піднесення обох частин до парного степеня можуть з’явитися побічні корені. Це відбувається за рахунок того, що при піднесенні обох частин початкового рівняння ![]() до парного степеня дістаємо рівняння, що є результатом не тільки рівняння
до парного степеня дістаємо рівняння, що є результатом не тільки рівняння ![]() , але і рівняння
, але і рівняння ![]() , оскільки і
, оскільки і ![]() , і
, і ![]() . Так, наприклад, візьмемо рівняння
. Так, наприклад, візьмемо рівняння ![]() . Піднісши обидві частини цього рівняння до квад-рата, дістанемо
. Піднісши обидві частини цього рівняння до квад-рата, дістанемо ![]()
![]()
![]() Коренями цього рівняння є числа
Коренями цього рівняння є числа ![]()
![]() Однак після перевірки переконуємось, що
Однак після перевірки переконуємось, що ![]() є коренем рівняння
є коренем рівняння ![]() , а
, а ![]() є побічним коренем.
є побічним коренем.
Приступаючи до розв’язання ірраціонального рівняння, що містить парні степені радикалів, буває корисним знаходження області допустимих значень (ОДЗ), це, як правило, полегшує розв’язування рівняння. Якщо робити лише еквівалентні перетворення, то перевірку робити не потрібно.
Розглянемо рівняння виду ![]() . Очевидно, що ліва частина рівняння, яка містить радикал парного степеня, не може бути від’ємна, а отже невід’ємна і права частина даного рівняння. Враховуючи область допустимих значень, підкореневий вираз також не може бути від’ємним. Отже, рівняння виду
. Очевидно, що ліва частина рівняння, яка містить радикал парного степеня, не може бути від’ємна, а отже невід’ємна і права частина даного рівняння. Враховуючи область допустимих значень, підкореневий вираз також не може бути від’ємним. Отже, рівняння виду ![]() рівносильне такій системі:
рівносильне такій системі:
![]()
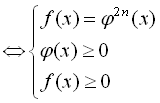 .
.
У системі Maple ірраціональні рівняння, як і раціональні, розв’язу-ються за допомогою функції solve(). Для позначення кореня використовуємо функцію sqrt ().
Приклад 1. Розв’язати рівняння ![]() .
.
Розв’язання
Дане рівняння можна звести до вигляду ![]() , тобто
, тобто ![]()
![]()
![]()
![]()
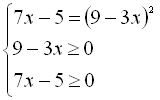
![]()
![]()
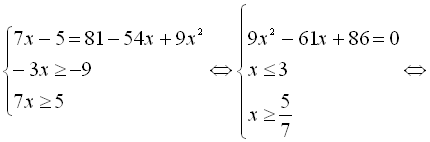
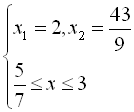 .
.
З даної системи випливає, що лише ![]() є коренем початкового рівняння.
є коренем початкового рівняння.
Розв’язання рівняння виду ![]() , де
, де ![]() , здійснюється піднесенням обох частин рівняння до квадрату, «ізолюванням» радикала, який при цьому отримується, і повторним піднесенням обох частин рівняння до квадрата. В результаті таких перетворень рівняння даного виду зводиться до раціонального.
, здійснюється піднесенням обох частин рівняння до квадрату, «ізолюванням» радикала, який при цьому отримується, і повторним піднесенням обох частин рівняння до квадрата. В результаті таких перетворень рівняння даного виду зводиться до раціонального.
Приклад 2. Розв’язати рівняння ![]() .
.
Розв’язання
Область визначення даного рівняння визначається в результаті розв’-
язання системи нерівностей 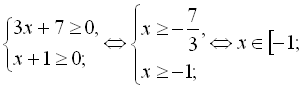
![]() .
.
Перетворимо дане рівняння:
![]()
![]()
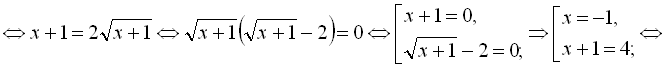
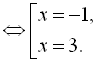
Обидва знайдені корені належать ОДЗ.
Відповідь: ![]()
![]() .
.
Приклад 3. Розв’язати рівняння ![]() .
.
Розв’язання
Знайдемо для початку область допустимих значень: 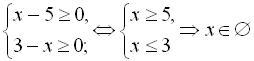 .
.
Оскільки область допустимих значень виявилась пустою множиною, то і розв’язків дане рівняння не має.
Відповідь: ![]() .
.
Приклад 4. Розв’язати рівняння ![]() .
.
Розв’язання
Обидва підкореневі вирази є повними квадратами, тому
![]()
![]()
Тобто дане ірраціональне рівняння звелося до раціонального рівняння з двома модулями.
Приклад розв’язання рівняння такого типу наводився раніше.
Відповідь: ![]()
![]() .
.
Рівняння виду ![]() можна розписати за допомогою змішаних систем:
можна розписати за допомогою змішаних систем:
![]()
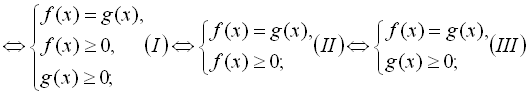
З наведених вище трьох систем вибирають звичайно ту, де простіше розв’язати нерівність (![]() або
або ![]() ). Якщо ж обидві нерівності
). Якщо ж обидві нерівності ![]() і
і ![]() розв’язати нескладно, то можна вибрати першу систему, яка хоча і містить одну зайву нерівність, є більш наочною, ніж ІІ і ІІІ.
розв’язати нескладно, то можна вибрати першу систему, яка хоча і містить одну зайву нерівність, є більш наочною, ніж ІІ і ІІІ.
Приклад 5. Розв’язати рівняння ![]() .
.
Розв’язання
Для розв’язання даного рівняння обираємо ІІІ систему:
![]()
![]()
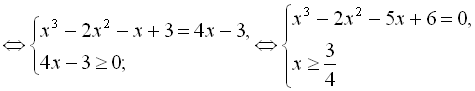 .
.
Окремо розв’яжемо рівняння ![]() нашої системи. Методом підбору знаходимо цілий корінь даного рівняння. Для цього виписуємо дільники вільного члена: ±1; ±2; ±3. При підборі знаходимо, що коренями є -2; 1; 3. Тоді
нашої системи. Методом підбору знаходимо цілий корінь даного рівняння. Для цього виписуємо дільники вільного члена: ±1; ±2; ±3. При підборі знаходимо, що коренями є -2; 1; 3. Тоді 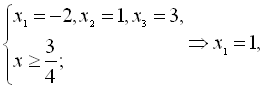
![]()
Відповідь: ![]()
![]()
3),x=-2);
Приклад 6. Розв’язати рівняння ![]() .
.
Розв’язання
Піднесемо обидві частини початкового рівняння до п’ятого степеня, дістанемо: ![]() , звідки
, звідки ![]() .
.
Перевірка: Підставивши ![]() в початкове рівняння, дістанемо
в початкове рівняння, дістанемо ![]() , тобто
, тобто ![]() – правильна рівність
– правильна рівність ![]() є коренем.
є коренем.
Відповідь: ![]() .
.
Приклад 7. Розв’язати рівняння ![]() .
.
Розв’язання
ОДЗ початкового рівняння – всі дійсні числа. Піднесемо обидві частини рівняння до кубу:
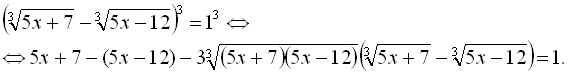
Замінимо різницю ![]() правою частиною первинного рівняння, тобто 1:
правою частиною первинного рівняння, тобто 1: ![]() .
.
Ізолюємо кубічний корінь, що залишився, і піднесемо обидві частини рівняння до кубу: ![]()
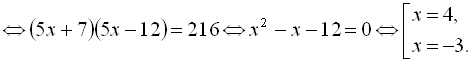
Виконавши перевірку, знайдемо, що множиною розв’язків даного рівняння є ![]()
![]() .
.
Відповідь: ![]()
![]() .
.
Способи розв'язання ірраціональних нерівностей:
- Розв’язування найпростіших ірраціональних нерівностей.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , розв’язків немає
, розв’язків немає
Приклад 1. Розв’яжіть нерівність ![]() .
.
Розв’язання. Задана нерівність рівносильна нерівності ![]() .
.
Відповідь: ![]() .
.
- Спосіб рівносильних перетворень:
-
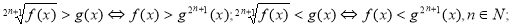
-
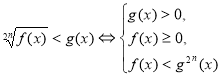 .
.
Приклад 2. Розв’яжіть нерівність ![]() .
.
Розв’язання. Нерівність рівносильна системі нерівностей:
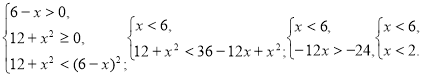
Відповідь: ![]() .
.
Приклад 3. Розв’яжіть нерівність ![]() .
.
Розв’язання. Нерівність рівносильна сукупності нерівностей
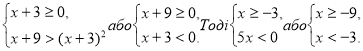
Відповідь: ![]() .
.
- Метод інтервалів.
Приклад 4. Розв’яжіть нерівність ![]() .
.
Розв’язання. ОДЗ нерівності ![]() . Задана нерівність рівносильна нерівності
. Задана нерівність рівносильна нерівності ![]() . Позначимо
. Позначимо ![]() . Нулі функції
. Нулі функції ![]() . На області визначення функції позначимо її нулі й на здобутих проміжках визначимо знаки функції:
. На області визначення функції позначимо її нулі й на здобутих проміжках визначимо знаки функції:
![]()
Відповідь: ![]() .
.
Виконуемо завдання
Тестуванняhttps://vseosvita.ua/test/start/npd124 8б
Рівняння називається тригонометричним, якщо невідома величина знаходиться під знаком тригонометричних функцій. Найпростішими тригонометричними рівняннями називаються рівняння 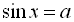 ,
, 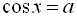 ,
, 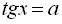 ,
, 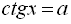 . Розв’язати найпростіше тригонометричне рівняння – означає знайти множину всіх кутів, що мають дане значення
. Розв’язати найпростіше тригонометричне рівняння – означає знайти множину всіх кутів, що мають дане значення 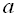 тригонометричної функції. Якщо тригонометричне рівняння не є найпростішим, то за допомогою тотожних перетворень його треба звести до одного або кількох найпростіших, розв’язання яких визначається стандартними формулами.
тригонометричної функції. Якщо тригонометричне рівняння не є найпростішим, то за допомогою тотожних перетворень його треба звести до одного або кількох найпростіших, розв’язання яких визначається стандартними формулами.
При використанні формул для розв’язування тригонометричних рівнянь враховуйте, що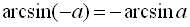 ;
; 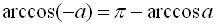 ;
;
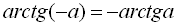 ;
; 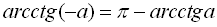 .
.
Прередивіться відео уроки
1.Найпростіші рівняння
2.Квадратні та такі,що зводяться до квадратних
Рівняння називається тригонометричним, якщо невідома величина знаходиться під знаком тригонометричних функцій. Найпростішими тригонометричними рівняннями називаються рівняння ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Розв’язати найпростіше тригонометричне рівняння – означає знайти множину всіх кутів, що мають дане значення
. Розв’язати найпростіше тригонометричне рівняння – означає знайти множину всіх кутів, що мають дане значення ![]() тригонометричної функції. Якщо тригонометричне рівняння не є найпростішим, то за допомогою тотожних перетворень його треба звести до одного або кількох найпростіших, розв’язання яких визначається стандартними формулами.
тригонометричної функції. Якщо тригонометричне рівняння не є найпростішим, то за допомогою тотожних перетворень його треба звести до одного або кількох найпростіших, розв’язання яких визначається стандартними формулами.
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Прередивіться відео уроки
1.Найпростіші рівняння
2.Квадратні та такі,що зводяться до квадратних
Способи розв'язування тригонометричних рівнянь
1) Заміна змінних при розв’язуванні тригонометричних рівнянь
Сьогодні ми навчимось розв’язувати складніші тригонометричні рівняння, які шляхом поточних перетворень можна звести до рівнянь з однією тригонометричною функцією, потім зробити заміну і звести до алгебраїчного рівняння.
Приклад 1. Розв’язати рівняння
2 sin2x + sinx – 1 = 0
В ході пояснення задаю питання учням, спонукаю до спільного обговорення розв’язку, учні записують розв’язання у зошит.
Розв’язання.
Введемо нову змінну t = sin x.
Оскільки sin x – функція обмежена, то t ϵ [-1;1]
Тоді дане рівняння буде мати вигляд 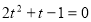 .
.
Розв’яжемо його: 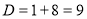 ,
, 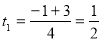 ,
, 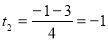 .
.
Тому, 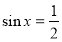 або
або 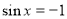 .
.
1) 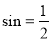 ,
,
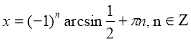 ,
,
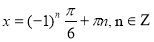 .
.
2) 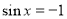 ,
,
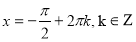 .
.
Відповідь: 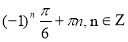 ,
, 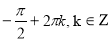 .
.
2) Розв’язування тригонометричних рівнянь зведенням до однієї функції (з однаковим аргументом).
Приклад 2. Розв’язати рівняння
6sin2x + 5cosx – 2 = 0
Обговорюється хід розв’язування рівняння, проектується розв’язання, записують у зошит.
Замінимо  на
на 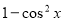 і отримаємо квадратне рівняння відносно
і отримаємо квадратне рівняння відносно 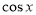 .
.
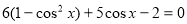 ,
,
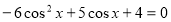 ,
,
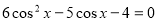 .
.
Нехай 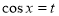 ,
, 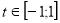 , тоді
, тоді 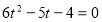 ,
, 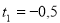 ,
, 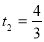 - сторонній корінь. Отже,
- сторонній корінь. Отже, 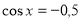 ,
,
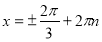 ,
, 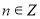 .
.
Відповідь: 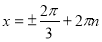 ,
, 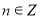 .
.
Алгоритм розв’язування рівнянь зведенням до однієї функції (з однаковим аргументом).
- Спробувати всі тригонометричні функції звести до одного аргументу.
- Якщо вдалося звести до одного аргументу, то спробувати всі тригонометричні вирази звести до однієї функції.
- Зробити заміну.
- Звести рівняння до квадратного.
- Розв’язати квадратне рівняння.
- Повернутись до заміни і розв’язати утворені рівняння.
- Записати відповідь.
Приклад 3. Розв’язати рівняння 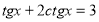
Чи можна це рівняння записати відносно однієї тригонометричної функції? Виконайте це.
Чи можна це рівняння записати у вигляді квадратного рівняння відносно однієї змінної?
Розв’яжіть рівняння, перевірте правильність виконання, виправте помилки.
Розв’язання. Оскільки 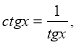 то рівняння можна записати у вигляді
то рівняння можна записати у вигляді
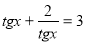 .
.
Позначимо 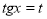 . Отримаємо рівняння
. Отримаємо рівняння 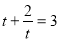 , яке зводиться до квадратного
, яке зводиться до квадратного
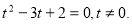
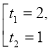
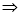
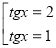
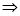
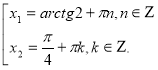
Відповідь: 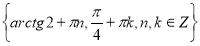 .
.
3) Розв’язання тригонометричних рівнянь за допомогою розкладання на множники.
Приклад 4. Розв’язати рівняння 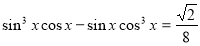 .
.
Розв'язання. У лівій частині рівняння винесемо за дужки спільний множник і застосуємо формули подвійного кута:  ,
,
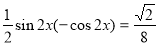 ,
,
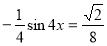 ,
,
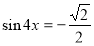 ,
,
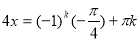 ,
, 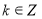 ;
;
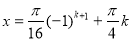 ,
, 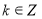 .
.
Відповідь: 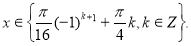
4) Однорідні тригонометричні рівняння.
Якщо всі члени рівняння у лівій і правій частинах якого стоять многочлени від двох змінних (або від двох функцій однієї змінної) мають однаковий сумарний степінь, то рівняння називається однорідним. Розв’язують однорідне рівняння діленням на найвищий степінь однієї змінної.
Зауваження. Дотримуючись цього орієнтира, доводиться ділити обидві частини рівняння на вираз зі змінною. При цьому можлива втрата коренів, якщо коренями є числа, при яких дільник дорівнює нулю. Щоб уникнути втрати коренів, необхідно окремо розглянути випадок, коли вираз, на який ми збираємось ділити обидві частини рівняння, дорівнював нулю, і лише після цього виконувати ділення на вираз що не дорівнює нулю.
Розглянемо рівняння виду 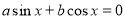 (однорідне рівняння 1-го степеня), де а і b не дорівнюють нулю. Значення х, при яких cos x дорівнює нулю, не задовольняє даному рівнянню, бо тоді і sin x теж дорівнював би нулю, а cos x і sin x не можуть одночасно дорівнювати нулю. Тому можна розділити обидві частини рівняння почленно на cos x. Маємо:
(однорідне рівняння 1-го степеня), де а і b не дорівнюють нулю. Значення х, при яких cos x дорівнює нулю, не задовольняє даному рівнянню, бо тоді і sin x теж дорівнював би нулю, а cos x і sin x не можуть одночасно дорівнювати нулю. Тому можна розділити обидві частини рівняння почленно на cos x. Маємо: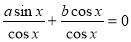 ,
, 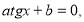
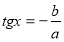 .
.
Розв’язавши дане тригонометричне рівняння отримуємо корені.
Рівняння виду
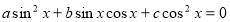
називається однорідним рівнянням 2-го степеня.
Якщо числа a, b, c не дорівнюють нулю, то розділимо дане рівняння на 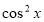 (або на
(або на 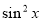 ). (У даному рівнянні
). (У даному рівнянні 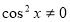 , бо в супротивному випадку
, бо в супротивному випадку 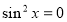 , а cos x і sin x не можуть одночасно дорівнювати нулю). Тоді
, а cos x і sin x не можуть одночасно дорівнювати нулю). Тоді
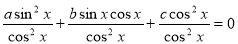
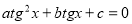 .
.
Розв'язавши отримане, рівняння одержимо корені даного рівняння.
Приклад 5. Розв’язати на дошці, коментуючи кожен крок. Залучати студентів до обговорення.
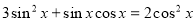
ОДЗ: 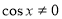
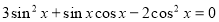 ділимо на
ділимо на 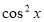
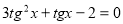
Заміна 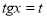 ,
, 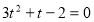 ,
, 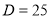 ,
, 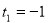 ,
, 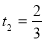 .
.
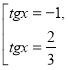
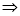

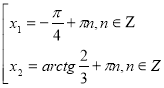
Відповідь: 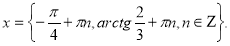
5. Метод введення допоміжного кута.
Розглянемо рівняння виду asinx + bcosx = c. Очевидно, що  .
.
Поділимо обидві частини рівняння на  і покладемо
і покладемо 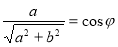 та
та 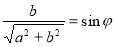 , маємо рівняння
, маємо рівняння 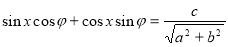 , або
, або 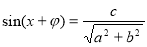 . Отже, дістали просте тригонометричне рівняння яке має розв’язки за умови
. Отже, дістали просте тригонометричне рівняння яке має розв’язки за умови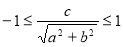 .
.
Виконуємо завдання
11.09.23 Домашне завдання :
.
- Встановіть відповідність між рівнянням і методом розв’язання.
- Розв’яжіть рівняння.(вибрати з таблиці та розв'язати одне рівняння на кожен з методів)
Рівняння
Методи
1) 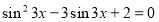
А) Зведення до однорідного рівняння n-го степеня.
2) 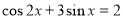
Б) Метод введення допоміжного кута.
3) 
В) Заміна змінних
4) 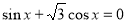
Г) Метод розкладання на множники.
5) 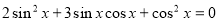
Д) Метод зведення до однієї функції (з однаковим аргументом).
6) 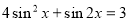
Е) Заміна змінних
7) 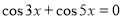
8) 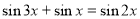
9) 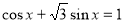
13.09.23
Ірраціональні ріняння та нерівності
Теоритичні відомості Рівняння
Способи розв'язування тригонометричних рівнянь
1) Заміна змінних при розв’язуванні тригонометричних рівнянь
Сьогодні ми навчимось розв’язувати складніші тригонометричні рівняння, які шляхом поточних перетворень можна звести до рівнянь з однією тригонометричною функцією, потім зробити заміну і звести до алгебраїчного рівняння.
Приклад 1. Розв’язати рівняння
2 sin2x + sinx – 1 = 0
В ході пояснення задаю питання учням, спонукаю до спільного обговорення розв’язку, учні записують розв’язання у зошит.
Розв’язання.
Введемо нову змінну t = sin x.
Оскільки sin x – функція обмежена, то t ϵ [-1;1]
Тоді дане рівняння буде мати вигляд ![]() .
.
Розв’яжемо його: ![]() ,
, ![]() ,
, ![]() .
.
Тому, ![]() або
або ![]() .
.
1) ![]() ,
,
![]() ,
,
![]() .
.
2) ![]() ,
,
![]() .
.
Відповідь: ![]() ,
, ![]() .
.
2) Розв’язування тригонометричних рівнянь зведенням до однієї функції (з однаковим аргументом).
Приклад 2. Розв’язати рівняння
6sin2x + 5cosx – 2 = 0
Обговорюється хід розв’язування рівняння, проектується розв’язання, записують у зошит.
Замінимо ![]() на
на ![]() і отримаємо квадратне рівняння відносно
і отримаємо квадратне рівняння відносно ![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
Нехай ![]() ,
, ![]() , тоді
, тоді ![]() ,
, ![]() ,
, ![]() - сторонній корінь. Отже,
- сторонній корінь. Отже, ![]() ,
,
![]() ,
, ![]() .
.
Відповідь: ![]() ,
, ![]() .
.
Алгоритм розв’язування рівнянь зведенням до однієї функції (з однаковим аргументом).
- Спробувати всі тригонометричні функції звести до одного аргументу.
- Якщо вдалося звести до одного аргументу, то спробувати всі тригонометричні вирази звести до однієї функції.
- Зробити заміну.
- Звести рівняння до квадратного.
- Розв’язати квадратне рівняння.
- Повернутись до заміни і розв’язати утворені рівняння.
- Записати відповідь.
Приклад 3. Розв’язати рівняння ![]()
Чи можна це рівняння записати відносно однієї тригонометричної функції? Виконайте це.
Чи можна це рівняння записати у вигляді квадратного рівняння відносно однієї змінної?
Розв’яжіть рівняння, перевірте правильність виконання, виправте помилки.
Розв’язання. Оскільки ![]() то рівняння можна записати у вигляді
то рівняння можна записати у вигляді
![]() .
.
Позначимо ![]() . Отримаємо рівняння
. Отримаємо рівняння ![]() , яке зводиться до квадратного
, яке зводиться до квадратного![]()
![]()
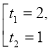
![]()
![]()
![]()
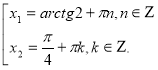
Відповідь: ![]() .
.
3) Розв’язання тригонометричних рівнянь за допомогою розкладання на множники.
Приклад 4. Розв’язати рівняння ![]() .
.
Розв'язання. У лівій частині рівняння винесемо за дужки спільний множник і застосуємо формули подвійного кута: ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
, ![]() ;
;
![]() ,
, ![]() .
.
Відповідь: ![]()
4) Однорідні тригонометричні рівняння.
Якщо всі члени рівняння у лівій і правій частинах якого стоять многочлени від двох змінних (або від двох функцій однієї змінної) мають однаковий сумарний степінь, то рівняння називається однорідним. Розв’язують однорідне рівняння діленням на найвищий степінь однієї змінної.
Зауваження. Дотримуючись цього орієнтира, доводиться ділити обидві частини рівняння на вираз зі змінною. При цьому можлива втрата коренів, якщо коренями є числа, при яких дільник дорівнює нулю. Щоб уникнути втрати коренів, необхідно окремо розглянути випадок, коли вираз, на який ми збираємось ділити обидві частини рівняння, дорівнював нулю, і лише після цього виконувати ділення на вираз що не дорівнює нулю.
Розглянемо рівняння виду ![]() (однорідне рівняння 1-го степеня), де а і b не дорівнюють нулю. Значення х, при яких cos x дорівнює нулю, не задовольняє даному рівнянню, бо тоді і sin x теж дорівнював би нулю, а cos x і sin x не можуть одночасно дорівнювати нулю. Тому можна розділити обидві частини рівняння почленно на cos x. Маємо:
(однорідне рівняння 1-го степеня), де а і b не дорівнюють нулю. Значення х, при яких cos x дорівнює нулю, не задовольняє даному рівнянню, бо тоді і sin x теж дорівнював би нулю, а cos x і sin x не можуть одночасно дорівнювати нулю. Тому можна розділити обидві частини рівняння почленно на cos x. Маємо:![]() ,
, ![]()
![]() .
.
Розв’язавши дане тригонометричне рівняння отримуємо корені.
Рівняння виду
![]()
називається однорідним рівнянням 2-го степеня.
Якщо числа a, b, c не дорівнюють нулю, то розділимо дане рівняння на ![]() (або на
(або на ![]() ). (У даному рівнянні
). (У даному рівнянні ![]() , бо в супротивному випадку
, бо в супротивному випадку ![]() , а cos x і sin x не можуть одночасно дорівнювати нулю). Тоді
, а cos x і sin x не можуть одночасно дорівнювати нулю). Тоді
![]()
![]() .
.
Розв'язавши отримане, рівняння одержимо корені даного рівняння.
Приклад 5. Розв’язати на дошці, коментуючи кожен крок. Залучати студентів до обговорення.
![]()
ОДЗ: ![]()
![]() ділимо на
ділимо на ![]()
![]()
Заміна ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
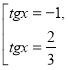
![]()
![]()
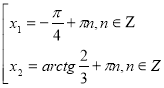
Відповідь: ![]()
5. Метод введення допоміжного кута.
Розглянемо рівняння виду asinx + bcosx = c. Очевидно, що ![]() .
.
Поділимо обидві частини рівняння на ![]() і покладемо
і покладемо ![]() та
та ![]() , маємо рівняння
, маємо рівняння ![]() , або
, або ![]() . Отже, дістали просте тригонометричне рівняння яке має розв’язки за умови
. Отже, дістали просте тригонометричне рівняння яке має розв’язки за умови![]() .
.
Виконуємо завдання
11.09.23 Домашне завдання :
.
- Встановіть відповідність між рівнянням і методом розв’язання.
- Розв’яжіть рівняння.(вибрати з таблиці та розв'язати одне рівняння на кожен з методів)
Рівняння | Методи |
1) | А) Зведення до однорідного рівняння n-го степеня.
|
2) | Б) Метод введення допоміжного кута. |
3) | В) Заміна змінних |
4) | Г) Метод розкладання на множники. |
5) | Д) Метод зведення до однієї функції (з однаковим аргументом). |
6) | Е) Заміна змінних |
7) |
|
8) |
|
9) |
|
13.09.23
Ірраціональні ріняння та нерівності
Ірраціональними називаються рівняння, у якиx змінна міститься під знаком кореня (радикала) або під знаком піднесення до дробового степеня.
В окремих випадках, не розв’язуючи дане ірраціональне рівняння, можна встановити, що воно не має коренів. Наприклад, рівняння 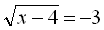 не має коренів, бо арифметичний корінь не може бути від’ємним.
не має коренів, бо арифметичний корінь не може бути від’ємним.
Рівняння 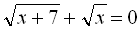 не має розв’язків, бо обидва доданки є арифметичними коренями, а тому не можуть бути від’ємними. А сума двох невід’ємних чисел дорівнює нулю лише тоді, коли кожен доданок дорівнює нулю. Одночасно ж вирази
не має розв’язків, бо обидва доданки є арифметичними коренями, а тому не можуть бути від’ємними. А сума двох невід’ємних чисел дорівнює нулю лише тоді, коли кожен доданок дорівнює нулю. Одночасно ж вирази 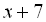 і
і 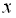 нулю дорівнювати не можуть.
нулю дорівнювати не можуть.
Основними методами розв’язування ірраціональних рівнянь є метод піднесення обох частин рівняння до одного і того самого степеня та метод введення нових змінних.
При розв’язуванні ірраціональних рівнянь методом піднесення обох частин до парного степеня можуть з’явитися побічні корені. Це відбувається за рахунок того, що при піднесенні обох частин початкового рівняння 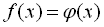 до парного степеня дістаємо рівняння, що є результатом не тільки рівняння
до парного степеня дістаємо рівняння, що є результатом не тільки рівняння 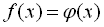 , але і рівняння
, але і рівняння 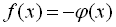 , оскільки і
, оскільки і 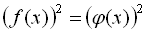 , і
, і 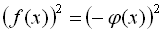 . Так, наприклад, візьмемо рівняння
. Так, наприклад, візьмемо рівняння 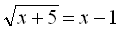 . Піднісши обидві частини цього рівняння до квад-рата, дістанемо
. Піднісши обидві частини цього рівняння до квад-рата, дістанемо 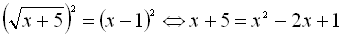
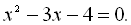 Коренями цього рівняння є числа
Коренями цього рівняння є числа 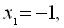
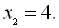 Однак після перевірки переконуємось, що
Однак після перевірки переконуємось, що 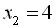 є коренем рівняння
є коренем рівняння 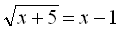 , а
, а 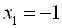 є побічним коренем.
є побічним коренем.
Приступаючи до розв’язання ірраціонального рівняння, що містить парні степені радикалів, буває корисним знаходження області допустимих значень (ОДЗ), це, як правило, полегшує розв’язування рівняння. Якщо робити лише еквівалентні перетворення, то перевірку робити не потрібно.
Розглянемо рівняння виду  . Очевидно, що ліва частина рівняння, яка містить радикал парного степеня, не може бути від’ємна, а отже невід’ємна і права частина даного рівняння. Враховуючи область допустимих значень, підкореневий вираз також не може бути від’ємним. Отже, рівняння виду
. Очевидно, що ліва частина рівняння, яка містить радикал парного степеня, не може бути від’ємна, а отже невід’ємна і права частина даного рівняння. Враховуючи область допустимих значень, підкореневий вираз також не може бути від’ємним. Отже, рівняння виду 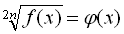 рівносильне такій системі:
рівносильне такій системі:
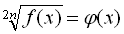
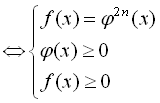 .
.
У системі Maple ірраціональні рівняння, як і раціональні, розв’язу-ються за допомогою функції solve(). Для позначення кореня використовуємо функцію sqrt ().
Приклад 1. Розв’язати рівняння 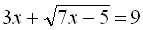 .
.
Розв’язання
Дане рівняння можна звести до вигляду 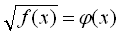 , тобто
, тобто 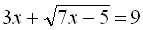
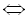
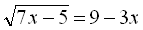
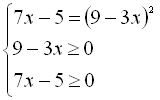
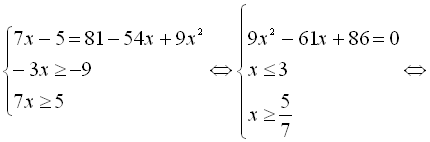
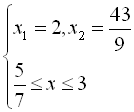 .
.
З даної системи випливає, що лише 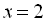 є коренем початкового рівняння.
є коренем початкового рівняння.
Розв’язання рівняння виду 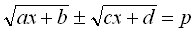 , де
, де 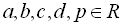 , здійснюється піднесенням обох частин рівняння до квадрату, «ізолюванням» радикала, який при цьому отримується, і повторним піднесенням обох частин рівняння до квадрата. В результаті таких перетворень рівняння даного виду зводиться до раціонального.
, здійснюється піднесенням обох частин рівняння до квадрату, «ізолюванням» радикала, який при цьому отримується, і повторним піднесенням обох частин рівняння до квадрата. В результаті таких перетворень рівняння даного виду зводиться до раціонального.
Приклад 2. Розв’язати рівняння 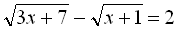 .
.
Розв’язання
Область визначення даного рівняння визначається в результаті розв’-
язання системи нерівностей 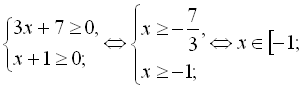
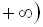 .
.
Перетворимо дане рівняння:
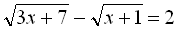
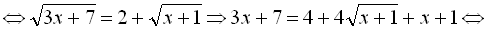
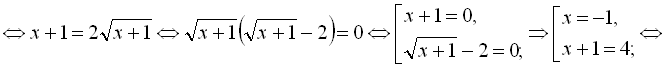
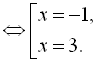
Обидва знайдені корені належать ОДЗ.
Відповідь: 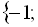
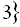 .
.
Приклад 3. Розв’язати рівняння 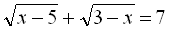 .
.
Розв’язання
Знайдемо для початку область допустимих значень: 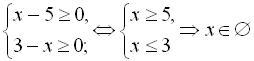 .
.
Оскільки область допустимих значень виявилась пустою множиною, то і розв’язків дане рівняння не має.
Відповідь:  .
.
Приклад 4. Розв’язати рівняння 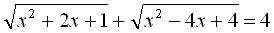 .
.
Розв’язання
Обидва підкореневі вирази є повними квадратами, тому
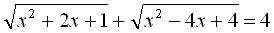
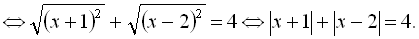
Тобто дане ірраціональне рівняння звелося до раціонального рівняння з двома модулями.
Приклад розв’язання рівняння такого типу наводився раніше.
Відповідь: 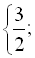
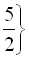 .
.
Рівняння виду 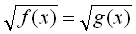 можна розписати за допомогою змішаних систем:
можна розписати за допомогою змішаних систем:
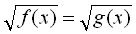
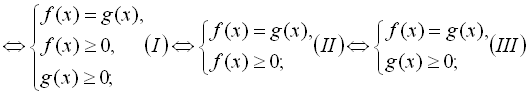
З наведених вище трьох систем вибирають звичайно ту, де простіше розв’язати нерівність (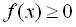 або
або 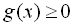 ). Якщо ж обидві нерівності
). Якщо ж обидві нерівності 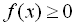 і
і 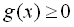 розв’язати нескладно, то можна вибрати першу систему, яка хоча і містить одну зайву нерівність, є більш наочною, ніж ІІ і ІІІ.
розв’язати нескладно, то можна вибрати першу систему, яка хоча і містить одну зайву нерівність, є більш наочною, ніж ІІ і ІІІ.
Приклад 5. Розв’язати рівняння 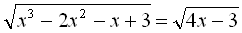 .
.
Розв’язання
Для розв’язання даного рівняння обираємо ІІІ систему:
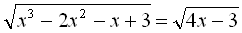
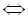
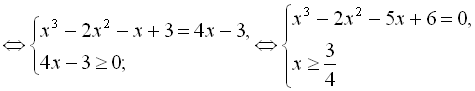 .
.
Окремо розв’яжемо рівняння 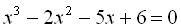 нашої системи. Методом підбору знаходимо цілий корінь даного рівняння. Для цього виписуємо дільники вільного члена: ±1; ±2; ±3. При підборі знаходимо, що коренями є -2; 1; 3. Тоді
нашої системи. Методом підбору знаходимо цілий корінь даного рівняння. Для цього виписуємо дільники вільного члена: ±1; ±2; ±3. При підборі знаходимо, що коренями є -2; 1; 3. Тоді 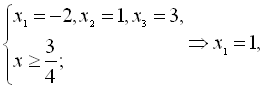
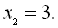
Відповідь: 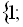
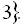
3),x=-2);
Приклад 6. Розв’язати рівняння 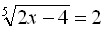 .
.
Розв’язання
Піднесемо обидві частини початкового рівняння до п’ятого степеня, дістанемо: 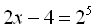 , звідки
, звідки 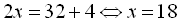 .
.
Перевірка: Підставивши 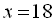 в початкове рівняння, дістанемо
в початкове рівняння, дістанемо 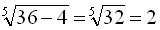 , тобто
, тобто 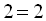 – правильна рівність
– правильна рівність 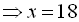 є коренем.
є коренем.
Відповідь: 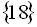 .
.
Приклад 7. Розв’язати рівняння 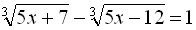 .
.
Розв’язання
ОДЗ початкового рівняння – всі дійсні числа. Піднесемо обидві частини рівняння до кубу:
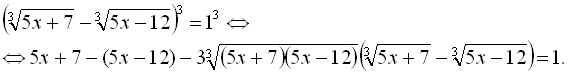
Замінимо різницю 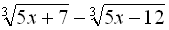 правою частиною первинного рівняння, тобто 1:
правою частиною первинного рівняння, тобто 1: 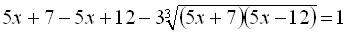 .
.
Ізолюємо кубічний корінь, що залишився, і піднесемо обидві частини рівняння до кубу: 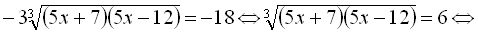
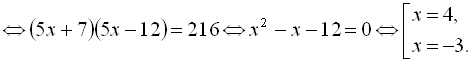
Виконавши перевірку, знайдемо, що множиною розв’язків даного рівняння є 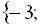
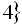 .
.
Відповідь: 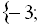
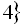 .
.
НерівностіСпособи розв'язання ірраціональних нерівностей:
- Розв’язування найпростіших ірраціональних нерівностей.
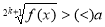
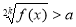
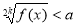
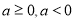
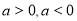
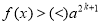
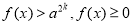
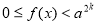 , розв’язків немає
, розв’язків немає
Приклад 1. Розв’яжіть нерівність 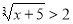 .
.
Розв’язання. Задана нерівність рівносильна нерівності 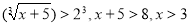 .
.
Відповідь: 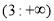 .
.
- Спосіб рівносильних перетворень:
-
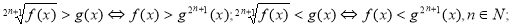
-
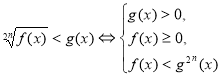 .
.
Приклад 2. Розв’яжіть нерівність 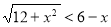 .
.
Розв’язання. Нерівність рівносильна системі нерівностей:
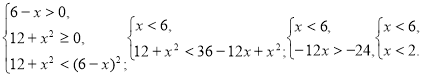
Відповідь: 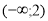 .
.
-

Приклад 3. Розв’яжіть нерівність 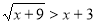 .
.
Розв’язання. Нерівність рівносильна сукупності нерівностей
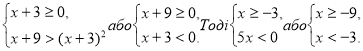
Відповідь: 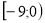 .
.
- Метод інтервалів.
Приклад 4. Розв’яжіть нерівність  .
.
Розв’язання. ОДЗ нерівності 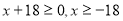 . Задана нерівність рівносильна нерівності
. Задана нерівність рівносильна нерівності 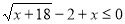 . Позначимо
. Позначимо 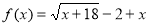 . Нулі функції
. Нулі функції 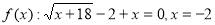 . На області визначення функції позначимо її нулі й на здобутих проміжках визначимо знаки функції:
. На області визначення функції позначимо її нулі й на здобутих проміжках визначимо знаки функції:

Відповідь: 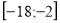 .
.
Виконуемо завдання
Тестуванняhttps://vseosvita.ua/test/start/npd124
Ірраціональними називаються рівняння, у якиx змінна міститься під знаком кореня (радикала) або під знаком піднесення до дробового степеня.
В окремих випадках, не розв’язуючи дане ірраціональне рівняння, можна встановити, що воно не має коренів. Наприклад, рівняння ![]() не має коренів, бо арифметичний корінь не може бути від’ємним.
не має коренів, бо арифметичний корінь не може бути від’ємним.
Рівняння ![]() не має розв’язків, бо обидва доданки є арифметичними коренями, а тому не можуть бути від’ємними. А сума двох невід’ємних чисел дорівнює нулю лише тоді, коли кожен доданок дорівнює нулю. Одночасно ж вирази
не має розв’язків, бо обидва доданки є арифметичними коренями, а тому не можуть бути від’ємними. А сума двох невід’ємних чисел дорівнює нулю лише тоді, коли кожен доданок дорівнює нулю. Одночасно ж вирази ![]() і
і ![]() нулю дорівнювати не можуть.
нулю дорівнювати не можуть.
Основними методами розв’язування ірраціональних рівнянь є метод піднесення обох частин рівняння до одного і того самого степеня та метод введення нових змінних.
При розв’язуванні ірраціональних рівнянь методом піднесення обох частин до парного степеня можуть з’явитися побічні корені. Це відбувається за рахунок того, що при піднесенні обох частин початкового рівняння ![]() до парного степеня дістаємо рівняння, що є результатом не тільки рівняння
до парного степеня дістаємо рівняння, що є результатом не тільки рівняння ![]() , але і рівняння
, але і рівняння ![]() , оскільки і
, оскільки і ![]() , і
, і ![]() . Так, наприклад, візьмемо рівняння
. Так, наприклад, візьмемо рівняння ![]() . Піднісши обидві частини цього рівняння до квад-рата, дістанемо
. Піднісши обидві частини цього рівняння до квад-рата, дістанемо ![]()
![]()
![]() Коренями цього рівняння є числа
Коренями цього рівняння є числа ![]()
![]() Однак після перевірки переконуємось, що
Однак після перевірки переконуємось, що ![]() є коренем рівняння
є коренем рівняння ![]() , а
, а ![]() є побічним коренем.
є побічним коренем.
Приступаючи до розв’язання ірраціонального рівняння, що містить парні степені радикалів, буває корисним знаходження області допустимих значень (ОДЗ), це, як правило, полегшує розв’язування рівняння. Якщо робити лише еквівалентні перетворення, то перевірку робити не потрібно.
Розглянемо рівняння виду ![]() . Очевидно, що ліва частина рівняння, яка містить радикал парного степеня, не може бути від’ємна, а отже невід’ємна і права частина даного рівняння. Враховуючи область допустимих значень, підкореневий вираз також не може бути від’ємним. Отже, рівняння виду
. Очевидно, що ліва частина рівняння, яка містить радикал парного степеня, не може бути від’ємна, а отже невід’ємна і права частина даного рівняння. Враховуючи область допустимих значень, підкореневий вираз також не може бути від’ємним. Отже, рівняння виду ![]() рівносильне такій системі:
рівносильне такій системі:
![]()
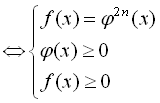 .
.
У системі Maple ірраціональні рівняння, як і раціональні, розв’язу-ються за допомогою функції solve(). Для позначення кореня використовуємо функцію sqrt ().
Приклад 1. Розв’язати рівняння ![]() .
.
Розв’язання
Дане рівняння можна звести до вигляду ![]() , тобто
, тобто ![]()
![]()
![]()
![]()
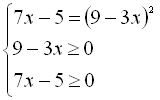
![]()
![]()
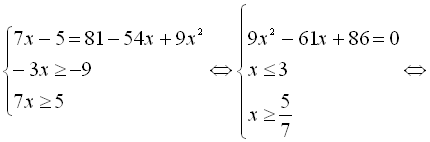
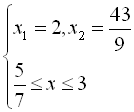 .
.
З даної системи випливає, що лише ![]() є коренем початкового рівняння.
є коренем початкового рівняння.
Розв’язання рівняння виду ![]() , де
, де ![]() , здійснюється піднесенням обох частин рівняння до квадрату, «ізолюванням» радикала, який при цьому отримується, і повторним піднесенням обох частин рівняння до квадрата. В результаті таких перетворень рівняння даного виду зводиться до раціонального.
, здійснюється піднесенням обох частин рівняння до квадрату, «ізолюванням» радикала, який при цьому отримується, і повторним піднесенням обох частин рівняння до квадрата. В результаті таких перетворень рівняння даного виду зводиться до раціонального.
Приклад 2. Розв’язати рівняння ![]() .
.
Розв’язання
Область визначення даного рівняння визначається в результаті розв’-
язання системи нерівностей 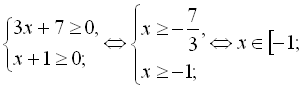
![]() .
.
Перетворимо дане рівняння:
![]()
![]()
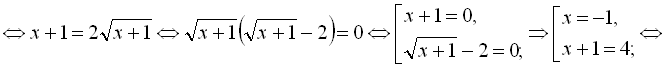
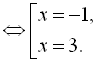
Обидва знайдені корені належать ОДЗ.
Відповідь: ![]()
![]() .
.
Приклад 3. Розв’язати рівняння ![]() .
.
Розв’язання
Знайдемо для початку область допустимих значень: 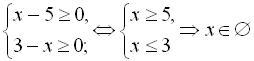 .
.
Оскільки область допустимих значень виявилась пустою множиною, то і розв’язків дане рівняння не має.
Відповідь: ![]() .
.
Приклад 4. Розв’язати рівняння ![]() .
.
Розв’язання
Обидва підкореневі вирази є повними квадратами, тому
![]()
![]()
Тобто дане ірраціональне рівняння звелося до раціонального рівняння з двома модулями.
Приклад розв’язання рівняння такого типу наводився раніше.
Відповідь: ![]()
![]() .
.
Рівняння виду ![]() можна розписати за допомогою змішаних систем:
можна розписати за допомогою змішаних систем:
![]()
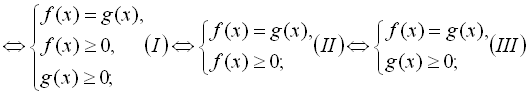
З наведених вище трьох систем вибирають звичайно ту, де простіше розв’язати нерівність (![]() або
або ![]() ). Якщо ж обидві нерівності
). Якщо ж обидві нерівності ![]() і
і ![]() розв’язати нескладно, то можна вибрати першу систему, яка хоча і містить одну зайву нерівність, є більш наочною, ніж ІІ і ІІІ.
розв’язати нескладно, то можна вибрати першу систему, яка хоча і містить одну зайву нерівність, є більш наочною, ніж ІІ і ІІІ.
Приклад 5. Розв’язати рівняння ![]() .
.
Розв’язання
Для розв’язання даного рівняння обираємо ІІІ систему:
![]()
![]()
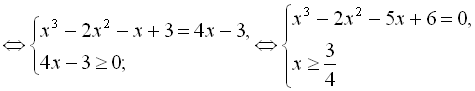 .
.
Окремо розв’яжемо рівняння ![]() нашої системи. Методом підбору знаходимо цілий корінь даного рівняння. Для цього виписуємо дільники вільного члена: ±1; ±2; ±3. При підборі знаходимо, що коренями є -2; 1; 3. Тоді
нашої системи. Методом підбору знаходимо цілий корінь даного рівняння. Для цього виписуємо дільники вільного члена: ±1; ±2; ±3. При підборі знаходимо, що коренями є -2; 1; 3. Тоді 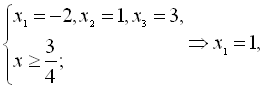
![]()
Відповідь: ![]()
![]()
3),x=-2);
Приклад 6. Розв’язати рівняння ![]() .
.
Розв’язання
Піднесемо обидві частини початкового рівняння до п’ятого степеня, дістанемо: ![]() , звідки
, звідки ![]() .
.
Перевірка: Підставивши ![]() в початкове рівняння, дістанемо
в початкове рівняння, дістанемо ![]() , тобто
, тобто ![]() – правильна рівність
– правильна рівність ![]() є коренем.
є коренем.
Відповідь: ![]() .
.
Приклад 7. Розв’язати рівняння ![]() .
.
Розв’язання
ОДЗ початкового рівняння – всі дійсні числа. Піднесемо обидві частини рівняння до кубу:
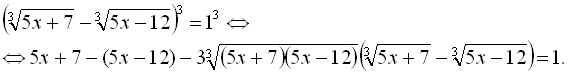
Замінимо різницю ![]() правою частиною первинного рівняння, тобто 1:
правою частиною первинного рівняння, тобто 1: ![]() .
.
Ізолюємо кубічний корінь, що залишився, і піднесемо обидві частини рівняння до кубу: ![]()
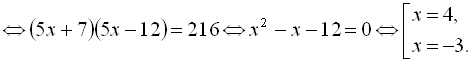
Виконавши перевірку, знайдемо, що множиною розв’язків даного рівняння є ![]()
![]() .
.
Відповідь: ![]()
![]() .
.
Способи розв'язання ірраціональних нерівностей:
- Розв’язування найпростіших ірраціональних нерівностей.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , розв’язків немає
, розв’язків немає
Приклад 1. Розв’яжіть нерівність ![]() .
.
Розв’язання. Задана нерівність рівносильна нерівності ![]() .
.
Відповідь: ![]() .
.
- Спосіб рівносильних перетворень:
-
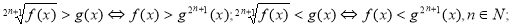
-
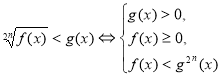 .
.
Приклад 2. Розв’яжіть нерівність ![]() .
.
Розв’язання. Нерівність рівносильна системі нерівностей:
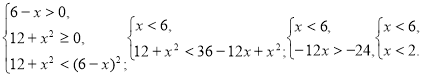
Відповідь: ![]() .
.
Приклад 3. Розв’яжіть нерівність ![]() .
.
Розв’язання. Нерівність рівносильна сукупності нерівностей
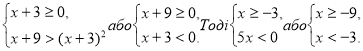
Відповідь: ![]() .
.
- Метод інтервалів.
Приклад 4. Розв’яжіть нерівність ![]() .
.
Розв’язання. ОДЗ нерівності ![]() . Задана нерівність рівносильна нерівності
. Задана нерівність рівносильна нерівності ![]() . Позначимо
. Позначимо ![]() . Нулі функції
. Нулі функції ![]() . На області визначення функції позначимо її нулі й на здобутих проміжках визначимо знаки функції:
. На області визначення функції позначимо її нулі й на здобутих проміжках визначимо знаки функції:
![]()
Відповідь: ![]() .
.
Виконуемо завдання
Тестуванняhttps://vseosvita.ua/test/start/npd124
































Комментариев нет:
Отправить комментарий