10 В Дистанційне навчання 2022 геометрия


2022-2023 навчальний рік
Працюємо дистанційно

Розпочався не дуже легкий навчальний рік,але ми все витримаємо!

Бажаю вам наснаги та наполегливості.Завжди рада вам допомогти.



 

1.Онлайн консультація  на платформі Google meet за розкладом 

2.Консультації та завдання на блогу


ІІ семестр
З Новим роком! Щастя, удачі, наполегливості у оволодінні математичною наукою.

24.05.23 Контрольна робота      4294338





15.05-19.05.23

Перетворення у просторі




Виконайте практичну роботу                                              
Побудуйте у просторі трикутник АВС з вершинами А (-2;3;0) В (4;-3;0) С(1;4;0).Виконайте послідовнно наступні перетворення:
1)побудуйте трикутник симетричний даному відносно початку координат
2) виконайте паралельне преренесеня отриманого трикутника, якщо воно задано наступним чином     х'= Х+2
                                   у' = у-1
                                    z`=z-2           
3)здійсніть поворот отриманого трикутника на кут 60 градусів відносно точкки
Д( 1;2;0)
Після кожного перетворення вкажіть координати вершин отриманого трикутника.

Скалярний добуток векторів. Кут між векторами.

Приєднайтесь до відео консультації
Передивіться запропановані відео уроки 
Розгляньте приклади



Виконате завдання №228



08.05-12.05.23

12.05 ДО 15.00
ТЕСТУВАННЯ:
 СКАЛЯРНИЙ ДОБУТОКhttps://vseosvita.ua/test/start/brp389

КООРДИНАТИ ВЕКТОРАhttps://vseosvita.ua/test/start/qdy062

Дії над векторами. Кут між векторами.

Приєднайтесь до відео консультації
Передивіться запропановані відео уроки 


Повторіть теоритичні відомості

Виконайте завдання:
1. Дано вектори а(2;4;-3) і в(х;1;6).При якому значені  Х кут між векторами а і в
а)гострий;  б) тупий;   в) прямий?
2. Знайти координати  вектора в колініарного вектору а (5;-3;4), якщо їх скалярний добуток дорівнює -100.
3. Точка К рівновіддалена від вершин квадрату АВСД з центром О .Виразіть через вектори КА, КВ і КС вектори АД, ДС, КД і КО.
4. Дано вектор а(-3;2;6) знайдіть координати вектора в , протилежно напрямленого з вектором а ,якщо ІвІ=21.

01.05-05.05.23

Дії над векторами.

Приєднайтесь до відео консультації
Передивіться запропановані відео уроки 



Попрацюйте з підручником
Пройдіть тестуванняhttps://vseosvita.ua/test/start/dld332

Вектори у просторі

Приєднайтесь до відео консультації
Передивіться запропановані відео уроки 


Попрацюйте з підручником


Розгляньте приклади

Виконайте завдання  №168,173(б)

Роботи надіслати електронною поштою  03.05 до 15.00




24.04-28.04.23

Рівняння прямої у просторі

Приєднайтесь до відео консультації
Передивіться запропановані відео уроки 





Попрацюйте з теоритичними відомостями



Завдання
Сласти рівняння прямої, що прходить через точки М(-5;-4;-6) і К( 2;-1;3)
Всі можливі випадки! 29.04 до 15.00

Рівняння прямої (повторення 9 клас)

Приєднайтесь до відео консультації
Передивіться запропановані відео уроки 



Повторіть теорію


Виконайте завдання
Рівняння скласти використовуючи два способи завдання прямої:
1) ах+ву=с
2)

Роботи надіслати електронною поштою.


17.04-20.04.23

Рівняння площини
21.04   Тестування    https://vseosvita.ua/test/start/zxb216    
Загальне    рівняння площини                                                                                                           
Особливі випадки                                                                                                   
Тестування    https://vseosvita.ua/test/start/zxb216                                                   

 

Рівняння сфери.Розв'язування вправ.

Приєднайтесь до відео консультації
Передивіться запропановані відео уроки 


Попрацюйте з теоритичними відомостями
Виконайте завдання

 19.04     14.00-15.00 відповіді надіслати електронною поштою

1. Визначте за рівнянням сфери координати її центра та радіус:

1) (х - 3)2 + (у + 7)2 + (z - 1)2 = 81;

2) х2 + у2 + (z + 5)2 = 19.

2. Складіть рівняння сфери із центром у точці А (-5; 2; 13) і радіусом R = 15.

3. Складіть рівняння сфери, діаметром якої є відрізок АВ, якщо А (-2; 3; 4), 

В (6; -3; 6).

4. Точки А (1; 0; z) і В(-1;у;0) належать сфері х2 + у2 + z2 = 10. Знайдіть довжину хорди АВ.

5.Доведіть, що рівняння х2 + у2+z2 + 2у – 6z - 6 = 0 є рівнянням сфери; 

укажіть координати центра і радіус цієї сфери.







10.04-14.04.23


14.04 тестування


12.04 до 14.00-15.00 
Виконайте завдання: №62(б), 63(а)
"Координати у просторі.Відстань між точками,координати середини відрізку"

Приєднайтесь до відео консультації
Передивіться запропановані відео уроки 







Пригадайте формули та властивості фігур



Виконайте завдання: №62(б), 63(а)









03.04-07.04.23

Тестування 07.04
Координати у просторі

Приєднайтесь до відео консультації
Передивіться запропановані відео уроки 

Попрацюйте з теоритичними відомостями    



Розгляньте приклад
Подумайте ,та виконайте завдання:
Завдання 1-3, у таблицю запишіть свої координати, які відповідають умовам

Підготуйте відповіді на питання                                                                 
Тестування                                                                                                                                       

20.03.-24.03.23
Узагальнення та систематизація знань.Контрольна робота.


Виконате контрольну роботу

Контрольна робота



Моделювання
Зробити модель за текстом задачі
№ 702   9 б

№705    12 б

15.03.-17.03.23

Ортогональне проєктування. Площа ортогональної проекції многокутника
 Приєднайтесь до відео консультації
Передивіться запропановані відео уроки                                                                              Попрацюйте з теоритичними відомостями      
   


Виконайте завдання  15.03 надіслати електронною поштою

Виконайте завдання  17.03  

задачі не треба! тільки тест! 

Перед виконанням тесту знайдіть відповідь на наступне питання:
Чому дорівнює площа рівнобічної трапеції, діагоналі якої перпендикулярні?

06.03.-10.03.23

Площа ортогональної проекції многокутника


Завдання:                                                                                                
№1 Після перегляду відео уроків виберіть та роз'яжіть будь які дві задачі                            


Перед виконанням тесту ,ще раз перегляньте §16


27.02-03.03.23

Ортогональне проекціювання. Площа ортогональної проекції многокутника

Передивіться запропановані відео уроки 
Попрацюйте з підручником


Розляньте приклади розв'язків задач
Дайте обгрунтовані відповіді на питання та розв'яжіть задачі


20.02-24.02.23

"Кути у просторі"

  Передивіться запропановані відео уроки 



   Попрацюйте з теоритичними відомостями        


тестування 

№1теоритичні відомості на визначення кутів та відстаней https://vseosvita.ua/test/start/bll138

№2 вимірювання кутів , площа ортоганальної проекції

13.02-17.02.23

"Перпендикулярні площини"
  Передивіться запропановані відео уроки                                                                              Попрацюйте з теоритичними відомостями                                                                        Складіть конспект до теми                                                                                                
Дайте відповідь на запитання №566-571                                                                               



  




Роботи надіслати електронною поштою 15.02!!!!!



06.02-10.02. 23                                                                                  
                                                                            
"Властивості точок рівновіддалених від вершин та сторін многокутника."
Онлайн консультація  на платформі Google meet за розкладом                                         
Корисні підказки                                                                                                                   
                                                                                                              



                                                        


Виконайте завдання№ 697,698     9б  або
                                      № 721,722    11б



30.01-03.02. 2023   
Дивись завдання №1,№2                                                                             
"Відстані у просторі.Властивості точок рівновіддалених від вершин та сторін многокутника."
Онлайн консультація  на платформі Google meet за розкладом                                         
Корисні підказки                                                                                                                 
                                                         


Завдання №1  Створити "слайд" за зразком(матеріал з планіметрії,стереометричні відомості,формули)
Роботи надіслати на електронну пошту


Завдання №2 тестування https://vseosvita.ua/test/start/ave042





23.01-27.01 2023                                                                                   
Завдання :                                                                                            
№1         №683 

Увага! час тестування 30 хвилин                                                                                                  №2     тестування    https://vseosvita.ua/test/start/pif976                                                                                                   
  "Відстані у просторі.Розв'язування задач"      
Онлайн консультація  на платформі Google meet за розкладом                       

Передивіться запропоновані відео уроки                                                          

                                                                             



Опрацюйте теритичні відомості                                                                                                               

 



Виконайте завдання:                                                                                                                       
№1 Відповіді на запитання №683   запишіть у вигляді таблиці                                                   

А

Б

В

Г

Д

Е

 

 

 

 

 

 

 

 

 
                                                                               

                                         


16.01-20.01 2023

"Теорема про три перпендикуляри"

Онлайн консультація  на платформі Google meet за розкладом 

Передивіться запропоновані відео уроки

Виконайте завдання:
№1 тестування https://vseosvita.ua/test/start/aab825
№2  №536,516 розв'язки надіслати електронною поштою.

18.01    13.00-15.00 працюємо по групах

    І група

ІІ група

ІІІ група

     Волович

Багірян

Борщевський

      Єлісєєва

Доценко

Копилов

     Кузнецов

Козіна

Кузьменко

    Олійник

Симоненко

Поліщенко

    Пузірьов

Шевченко

Романчук

    Чужбойска

 

Слинявська

     Щербаков

 

Смертенюк

 

 

Шулежко

    №  536,538,541

№ 517,519,521,524

№ 516,520, 522



"Теорема про три перпендикуляри"

Онлайн консультація  на платформі Google meet за розкладом 

Передивіться запропоновані відео уроки

13.01 Розв'яжи задачу


09.01-13.01 23
Питання до таблиці


"Перпендикулярність прямих.Прямої та площини.Теорема про три перпендикуляри"

Онлайн консультація  на платформі Google meet за розкладом 

Передивіться запропоновані відео уроки



Попрацюйте з підручником



Розгляньте приклади
Виконайте завдання:
№1 задачи 513,515                                                                                                        


№2 тестування







19.12-23.12.22

Контрольна робота за І семестр
☝
"Планіметричні задачі у курсі стериометрії"
Повторення осноаних властивостей плоских фігур:
формули,співвідношення,властивосі,ознаки рівності та подібності.



12.12-16.12.22

Всі завдання:

№1 Заповніть таблицю відповідей
№2 Виберіть та розв'яжить три задачі
"Паралельність у просторі. Розв'язування вправ."

Онлайн консультація  на платформі Google meet за розкладом 

Головне у вивчені теми
Передивіться тестові завдання
№1Заповніть таблицю відповідей (надіслати електронною поштою)

1

2

3

4

5

6

7

8

9

10

 

 

 

 

 

 

 

 

 

 
№2Виберіть та розв'яжить три (надіслати електронною поштою)




05.12-09.12.22

Всі завдання:

№1  задачі 1-3 
"Паралельність площин.Розв'язування вправ."

Онлайн консультація  на платформі Google meet за розкладом 

Передивіться запропоновані відео уроки




Завдання
№1 Зробіть малюнки за текстом задач і розв'яжіть їх

1.    Точки  , що належать площині α, є паралельними проекціями кінців відрізка  та його середини  на дану площину відповідно. Знайдіть довжину відрізка  якщо

2.   Паралельні прямі AB та CD перетинають площини  та  β  (α II β) так, що точки A і C належать α,  B і D належать β. Знайдіть довжини відрізків BD та CD , якщо AB=8 см, AC=5 см.

3.    Площини α та β - паралельні. Через точку S, що лежить поза ними, проведено дві прямі m та n так, що вони перетинають площину  у точках , площину β – у точках  відповідно. Знайдіть , якщо SE:EK=3:5, 

28.11-02.12.2022

Всі завдання:

№1 тестування https://vseosvita.ua/test/start/ddt501

№2  задача (дивись таблицю та виконуй свій номер)                                                                                                                                           

02.12 робота на уроці  (роботи надіслати електроною поштою до 05.12)

 

 

№

1

Багирян

266

2

Борщевский

256 а

3

Волович

270 а

4

Доценко

260

5

Елисеева

270 б

6

Козина

258

7

Копылов

259

8

Кузнецов

261

9

Кузьменко

262

10

Олейник

272

11

Полищенко

273

12

Пузырёв

269

13

Романчук

257

14

Симоненко

268

15

Слинявская

256 б

16

Смертинюк

263

17

Чужбойская

267

18

Шевченко

265

19

Шулежко

264

20

Щербаков

275

21

Питель

263


"Паралельність площин.Розв'язування вправ."

Онлайн консультація  на платформі Google meet за розкладом 

Передивіться запропоновані відео уроки

Розгляньте приклади розв'язування задач:



Виконайте завдання:
№1 тестування  https://vseosvita.ua/test/start/ddt501


21.11-25.11.2022
Всі завдання

№1 зробіть малюнок  роботи надіслати на пошту 

№2 тестування https://vseosvita.ua/test/start/cnr404 

Паралельність площин

Онлайн консультація  на платформі Google meet за розкладом 

Передивіться запропоновані відео уроки


Попрацюйте з теоритичними відомостями!                                                                             


№1  Розгляньте приклад побудови перерізу і за описом зробіть малюнок
роботи надіслати на пошту
Виконайте усно            №282-287                                                        
№2 Пройдіть тестування https://vseosvita.ua/test/start/cnr404      


14.11-18.11.2023
Всі завдання
№1  розв'яжіть задачі
№2 тестування  https://vseosvita.ua/test/start/aqf503
18.11.22 Практична робота   11.00-12.00
*Побудувати зображення кола вписаного в квадрат  (перед виконанням роботи передивіться відео урок)
!! спочатку побудувати овал.а потім квадрат ,описаний навколо нього.


 Взаємне розміщення прямої та площини у просторі.

Онлайн консультація  на платформі Google meet за розкладом 

Передивіться запропоновані відео уроки




Пригадайте дещо з теорії
Проконтролюйте себе, даючи відповіді на наступні питання


Пререйдіть до виконання завдань
№1 розв'яжіть задачі


№2 тестування https://vseosvita.ua/test/start/aqf503

 

07.11-11.11.2023
Всі завдання
№2   задачі 5,6
Взаємне розміщення прямої та площини у просторі.

Онлайн консультація  на платформі Google meet за розкладом 

Передивіться запропоновані відео уроки



Попрацюйте з підручником



Розв'яжить задачи (УСНО)
Виконайте завдання:
№2   задачі 5,6





26.10    12.00 тестування

28.10     10.00 Контрольна робота






"Взаємне розміщення двох прямих у просторі: прямі, що перетинаються; паралельні прямі;  мимобіжні прямі."
11.00 Онлайн консультація  на платформі Google meet за розкладом 
Передивіться відео уроки                                                              


17.10-21.10 2022
19.10 конспект


"Взаємне розміщення двох прямих у просторі: прямі, що перетинаються; паралельні прямі;  мимобіжні прямі."
Онлайн консультація  на платформі Google meet за розкладом 

Опрацювання теоритичних відомостей( конспект)


Опрацювання теоритичних відомостей( конспект)12.00
Дайте відповіді на запитання (письмово)
надіслати електроною поштою до 13.00
Питання №3: зобразьте приклади мимобіжих прямих(можна показати на многогранику)


"Взаємне розміщення двох прямих у просторі: прямі, що перетинаються; паралельні прямі;  мимобіжні прямі."


Онлайн консультація  на платформі Google meet за розкладом 

Передивіться запропоновані відео уроки




Попрацюйте з зошитами та підручником
Виконайте завдання:
№1(до 21.10)

№2 пройдіть тестування

https://vseosvita.ua/test/start/ora831



10.10-14.10 2022
14.10    11.00 Контрольна робота
ІІ задача на побубову
 
Побудувати переріз куба, який проходить через точки М,Р,К. Позначити буквами вершини куба.Запишить хід побудови.
Роботу надіслати електроною пошту до 12.00
      
    

"Побудова перерізів."

Приєднайтесь до відео консультації

Передивіться запропоновані відео уроки.

Передивіться презентацію

Опрацюйте важливі теоритичні факти

основні етапи розв’язування задач на побудову перерізів многогранників «методом слідів»:

Спосіб слідів  полягає в тому, що на площині нижньої основи ( іноді на якійсь іншій площині ) виконується побудова слідів ( ліній і точок перетину січної площини, деяких прямих ). За допомогою цих слідів легко виконується побудова точок перетину січної площини з ребрами многогранника та ліній перетину січної площини з гранями многогранника.

Розгляньте приклади розв'язків задач


Задача №1.

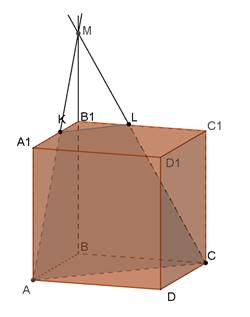
Побудувати переріз куба ABCDA1B1C1D1 площиною, яка проходить через вершини A, C і точку K, взяту на ребрі A1B1. Встановити види перерізу.

    

Розв’язання.

1)    Оскільки площина перерізу проходить через точки A  і C, то вона перетинає площину ABCD по прямій AC.

2)    (ABCD)||(A1B1C1D1), отже, площина перерізу перетинає площину A1B1C1D1  по прямій, яка паралельна прямій AC і проходить через точку K. Звідси проводимо KL||AC (LÎB1C1).

3)    AKLC – шуканий переріз.

 

4)    Многокутник AKLC – рівнобічна трапеція, так як:

а) AC||KL (AC і KL – основи трапеції).

б) Продовжимо AK і CL до перетину, одержимо: DABM=DCBM. Вони прямокутні, AB=CB, BM – спільний катет.

в) Звідси AM=CM, тому DAMC – рівнобедрений.

г) Оскільки KL||AC, то DKML – також рівнобедрений, тобто KM=LM.

д) Звідси випливає: AM-KM=CM-LM, тобто AK=CL.

 

 

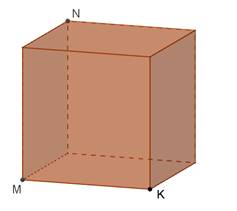
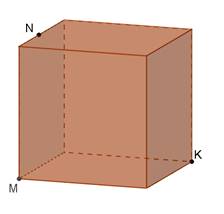
Задача №2.

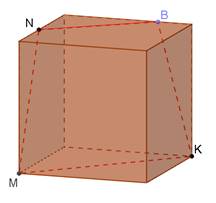
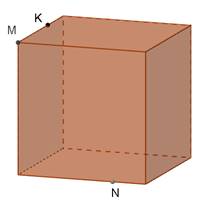
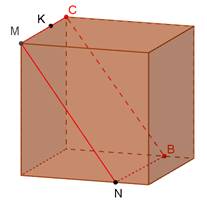
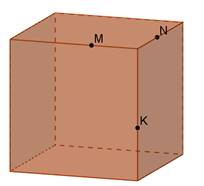
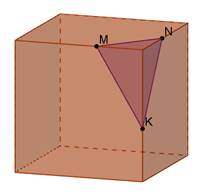
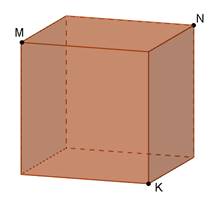
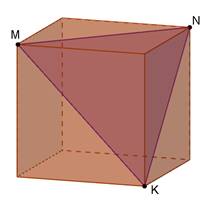
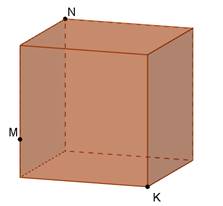
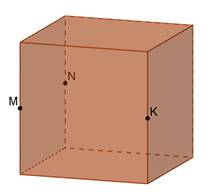
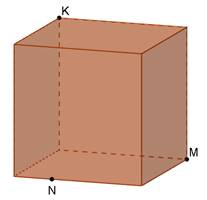
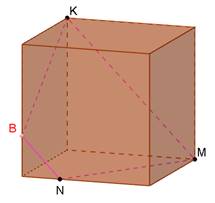
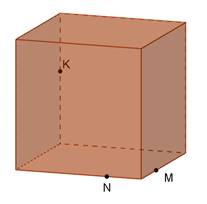
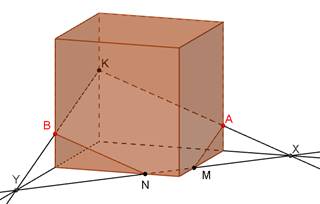
Дано куб. Побудувати перерізи куба площиною, що проходить через задані точки M, N, K. Встановити вид перерізу.

Розв’язання.

Використаємо властивість: паралельні площини перетинаються січною площиною по паралельних прямих.

 

 

1)

AKMN - прямокутник

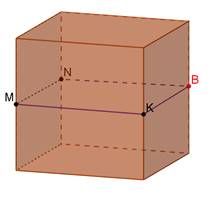
2)

MNBK – рівнобічна трапеція

3)

MCBN - прямокутник

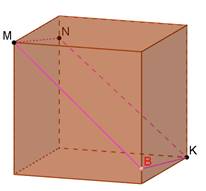
4)

MNK- трикутник

5)

MNK- рівносторонній трикутник

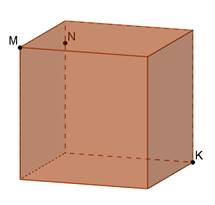
6)

MNAK - паралелограм

7) Точки M,N,K – середини відповідних ребер.

MNBK - квадрат

8)

MNKB - паралелограм

9)

MNBK – рівнобічна трапеція

 

10)

MNBKA – п’ятикутник

 

 

Задача №3.

Точки P,Q, R –середини ребер A1B1, B1C1 та CD куба ABCDA1B1C1D1. Який многокутник буде перерізом куба площиною PQR? Знайти площу цього многокутника, якщо відомо, що ребро куба дорівнює а.

Розв’язання.

                         

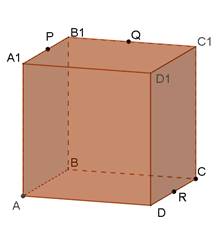
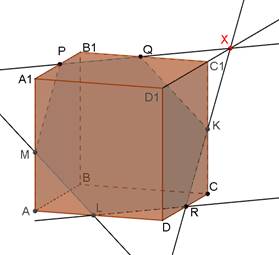
1)  Побудуємо переріз методом слідів. За теоремою про лінію перетину двох паралельних площин третьою площиною сторони перерізу, що лежать на паралельних гранях куба, паралельні. Трикутники PB1Q і QC1X рівні (чому?), тому , а так як  (чому?), то точка K – середина СС1 (чому?).

2)  Так як PQ||A1C1 (середня лінія DA1B1C1), RL||PQ (чому?), A1C1||AC, то LR||AC, отже, L – середина AD.

3)  Аналогічно, M- середина AA1.

4)  З рівності прямокутних трикутників MA1P, PB1Q, QC1K, KCR, RDL та LAM випливає, що всі сторони шестикутника PQKRLM рівні.

5)  З рівності прямокутних трикутників QC1X, XC1K, KC1Q слідує, що трикутник QKX рівносторонній, тому його кути дорівнюють 60°. Тоді \anglePQK=\angleQKR=180°-60°=120°.

6)  Аналогічно доводиться, що всі кути шестикутника PQKRLM дорівнюють 120°. Тому отриманий переріз є правильним шестикутником.

7) Сторона цього шестикутника дорівнює 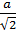  (чому?), отже, його площа дорівнює  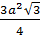(поясніть отриману відповідь). 

Виконайте завдання:

№1

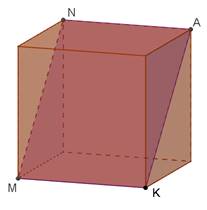
Побудуйте переріз куба ABCDA1B1C1D1 площиною, яка проходить через точки A, C, N, N ∈ A1D1 


 №2

Побудуйте переріз куба ABCDA1B1C1D1 площиною, яка проходить через точки D1, E, F, E ∈ AB, F ∈ В1С1 (див. рис. 3).


№3

Побудуйте переріз піраміди площиною, яка проходить через точки A, B і C 

Надіслати електронною поштою до 17.10

03.10-07.10. 2022

"Просторові геометричні фігури.Початкові уявлення про многогранники.Побудова перерізів."
Приєднайтесь до відео консультації

Передивіться запропоновані відео уроки.




Передивіться важливі теоритичні відомості

завдання№1,2 надіслати електронною поштою

Завдання №1

Побудувати переріз куба ABCDA1B1C1D1 площиною, яка проходить через вершини A, C і точку K, взяту на ребрі A1B1. Встановити види перерізу.

    За даними задачі і описом

побудуйте даний переріз

Розв’язання.

1)    Оскільки площина перерізу проходить через точки A  і C, то вона перетинає площину ABCD по прямій AC.

2)    (ABCD)||(A1B1C1D1), отже, площина перерізу перетинає площину A1B1C1D1  по прямій, яка паралельна прямій AC і проходить через точку K. Звідси проводимо KL||AC (LÎB1C1).

3)    AKLC – шуканий переріз.

 

4)    Многокутник AKLC – рівнобічна трапеція, так як:

а) AC||KL (AC і KL – основи трапеції).

б) Продовжимо AK і CL до перетину, одержимо: DABM=DCBM. Вони прямокутні, AB=CB, BM – спільний катет.

в) Звідси AM=CM, тому DAMC – рівнобедрений.

г) Оскільки KL||AC, то DKML – також рівнобедрений, тобто KM=LM.

д) Звідси випливає: AM-KM=CM-LM, тобто AK=CL.


  завдання №2

Задайте на ребрах куба три точки так,щоб перерізом куба був:

а) трикутник

б)чотирикутник

в)п'ятикутник

Побудувати !!!! 


26.09-30.09 2022
"Просторові геометричні фігури.Початкові уявлення про многогранники."

Передивіться важливі теоритичні відомості



Виконайте завдання:

19.09-23.09 2022
"Аксіоми стеріометрії"

Приєднайтесь до відеоуроку
Передивіться важливі теоритичні відомості

Аксіоми стереометрії

Основі поняття стереометрії. Аксіоми стереометрії

Основі поняття стереометрії. Аксіоми стереометрії

Основі поняття стереометрії. Аксіоми стереометрії


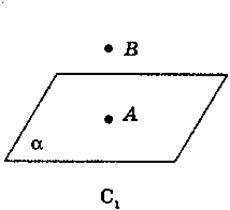
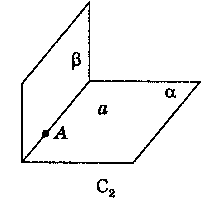
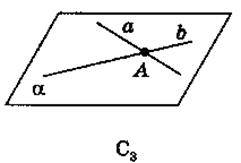
Передивіться відео уроки

Приклади розв'язування задач

Задача № 1. ст. 9 № 2.
Чи можна через точку перетину двох прямих провести третю пряму яка не лежить з ними на одній площині? Відповідь пояснить. 
Нехай прямі a іb перетинаються в точці m. Тоді згідно аксіоми С-3, через них можна провести площину a. За аксіомою С-1 завжди існують точки, які не належать площині a. Візьмемо точку N, що не належить площині a. Через дві точки можна провести пряму. Сполучимо точкиmі N. Пряма mN не належить площині a, але проходить через точку перетину прямих a іb. Отже, через точку перетину двох прямих можна провести третю пряму, яка не лежить з ними в одній площині.
Задача № 2.
Доведіть, що всі прямі, які перетинають дану пряму проходять через дану точку поза прямою, лежать в одній площині.
Нехай дано точку А і пряму а. Через дані пряму і точку можна провести площину. Нехай через точку А проходять прямі b, b1, b2, які перетинають пряму а, в точках B, B1, B2. Але всі точки прямої а належать площині a. Отримали, що кожна з даних прямих має з площиною дві спільні точки. Отже, прямі b, b1, b2 лежать в площині a.
Очевидно, що будь-яка пряма, яка проходить через точку А і перетинає пряму а, лежить в площині a.
Задача № 3. ст. 7 № 8.
Дано дві площини які не перетинаються. Доведіть, що пряма, яка перетинає одну з площин, перетинає й другу.
Площини a і b перетинаються. Пряма а перетинає площину a в точці А, або ΑÎа, АÎa. Доведемо, що пряма а перетинає площину b. Припустимо, що не перетинає площину β, тобто вони не мають спільних точок, тоді через дві точки на прямій а і одну точку на прямій b можна провести площину. Нехай ця припустима площина g проходить через точки А іB, що лежать на прямій а і точку С, що лежить на площині·b. Тоді площина g повинна перетнути площину b, по деякій прямій, що проходить через точку С, також повинна перетнути площину a по деякій прямій b, яка проходить через точку А (згідно аксіоми С-2). Отже прямі а і b перетинаються в точці А. У припустимій площині g лежать усі, три прямі а, b, с. Оскільки за нашим припущенням а не перетинає площину b, можемо стверджувати, що а не перетинає пряму с. Тоді за визначенням аксіоми випливає, що пряма b повинна перетинати пряму с. Але в цьому випадку площини a і b повинні мати спільну точку, тобто повинні перетинатись. Але це суперечить умові задачі. Отже, наше припущення не вірне. Тому пряма а перетинає площину b, що і треба було довести.
Задача № 3. ст. 9 № 12.
Дано чотири точки, що не лежать в одній площині. Скільки можна провести різних площин, які проходять через три з цих точок. Відповідь пояснить.
Нехай дано точки A, B, C, D, які не лежать в одній площині, тоді через будь-які три точки можна провести площину. Очевидно, що це будуть площини (ABC), (BCD), (ACD), (ABD). Отже, через чотири точки, що не лежать в одній площині можна провести чотири різні площини.
Задача № 4. ст. 10 № 14.
Дано чотири точки. Відомо, що пряма, яка проходить через будь-які з цих точок, не перетинається з прямою, яка проходить через інші точки. Доведіть, що дані чотири точки не лежать в одній площині.
ДОВЕДЕННЯ:(через показ презентації)
Припустимо, що точки A, B, C, D лежать в одній площині. Тоді прямі AB, CD, BC і AD (згідно умови) попарно паралельні, отже, вони є сторонами паралелограма ABCD. Але тоді діагоналі паралелограма AC і BD повинні перетинатися, що суперечить умові. Отже, наше припущення невірне і точки A, B, C, D не лежать в одній площині.

Пройдіть тестування 


Пройдіть тестування

Практична робота
Дано чотири точки, що не лежать в одній площині. Скільки можна провести різних площин, які проходять через три з цих точок. 
Відповідь проелюструйте та надішліть електронною поштою.

12.09-16.09 2022

          "Аксіоми   планіметрії  "

Приєднайтесь до відеоуроку
Передивіться важливі теоритичні відомості

 I. Аксіоми належності точок і прямих на площині

1. Яка б не була пряма, існують точки, що належать цій прямій, і точки, які не належать їй.

2. Через будь-які дві точки можна провести пряму, і тільки одну.

II. Аксіоми вимірювання

1. Кожен відрізок має певну довжину, виражену додатнім числом.

2. Довжина відрізка дорівнює сумі довжин частин, на які розбивається відрізок будь-якою своєю точкою.

3. Кожен кут має певну величину (градусну міру), виражену додатнім числом.

4. Величина розгорнутого кута становить 180°.

5. Величина кута дорівнює сумі величин кутів, на які розбивається даний кут променем, що виходить з вершини даного кута і проходить між його сторонами.

III. Аксіоми відкладання

1. Яка б не була півпряма, на ній від її початку можна відкласти відрізок заданої довжини, і тільки один.

2. Яка б не була півпряма, від неї в задану півплощину можна відкласти кут із заданою градусною мірою, і тільки один.

IV. Аксіоми взаємного розташування точок на прямій і площині

1. Які б не були три точки прямої, одна і тільки одна з них розташована між двома іншими.

2. Пряма розбиває площину на дві півплощини.

3. Якщо на площині проведена пряма і кінці відрізка належать одній з півплощин, то цей відрізок не перетинає пряму.

4. Якщо на площині проведена пряма і кінці відрізка належать різним півплощинам, то цей відрізок перетинає пряму.

V. Аксіома паралельності

  Через точку, що не належить прямій, можна провести пряму, паралельну даній, і тільки одну.         Виконай завдання   14.09.2022  10-В !

https://vseosvita.ua/test/start/tlp395

Заняття №3

12.09 10-В Діагностична контрольна робота 

Робота роспочнеться відповідно розкладу

  о 12.00,тривалість роботи 45 хвилин

https://vseosvita.ua/test/start/opp664 

      12.09-16.09 2022

    "Повторення.Прямокутний трикутник."

 
Приєднайтесь до відеоуроку
Передивіться важливі теоритичні відомості


 

 

 

Шукана сторона

Правило знаходження

Проти­лежний катет

Катет, протилежний до кута а, дорівнює:

• добутку гіпотенузи на sin α;

• добутку прилеглого катета на tg α

Прилег­лий

ка­тет

Катет, прилеглий до кута a, дорівнює:

• добутку гіпотенузи на cos α;

• відношенню протилежного кадета до tg α

Гіпоте­нуза


• відношенню протилежного катета до sin α;

• відношенню прилеглого катета до cos α

 
Виконай завдання

 
Виконання письмових вправ 

накресліть прямокутний трикутник ABC,∠С=90  (для задач 1-5)

1.    Розв'яжіть прямокутний трикутник за гіпотенузою і гострим кутом 

с = 8, α = 30°.

2.    Розв'яжіть прямокутний трикутник  за катетом і гострим кутом 

  а = 2, β = 45°.

3.    Розв'яжіть прямокутний трикутник  за гіпотенузою і катетом:   

   с = 9√2, а = 9.

4.    Розв'яжіть прямокутний трикутник  за двома катетами: а = 6√3, b = 6.

Виконуємо малюнки до задач!

5.    Відрізок BD — висота прямокутного трикутника ABC, проведена до гіпотенузи. Розв'яжіть трикутник ABC, якщо:

a) BD =6, ∠DBC = 60°;  ∠C = 30°.

6.    У рівнобічну трапецію вписано коло, радіус якого дорівнює 12 см. Знайдіть основи трапеції, якщо довжина бічної сторони дорівнює 25 см.

7.    У колі з центром О і радіусом 10 см проведено хорду АВ довжи­ною 16 см. Із центра кола до хорди проведено перпендикуляр, який перетинає хорду в точці Е, а коло — у точці F. Знайдіть довжину відрізка EF.

8.    Радіуси двох кіл дорівнюють 8 см і 3 см, а відстань між їх центра­ми — 13 см. Знайдіть довжину їх зовнішньої спільної дотичної.

 05.09-09.09 2022

       "Повторення.Прямокутний трикутник."

 
Приєднайтесь до відео консультації
Передивіться важливі теоритичні відомості
Виконай завдання

Передивіться запропоновані відео уроки.




Перейдіть до виконання завдань.
Задачи №2,3
 









Онлайн урок відбудеться  на платформі Google meet 

Четвер   11.00
12.05.2022 
"Координати у просторі.Довжина відрізку,середина відрізку.Вектори"

Приєднайтесь до відео консультації
Передивіться важливі теоритичні відомості
Виконай завдання Тест№4   https://vseosvita.ua/test/start/znw364



Підготовка до ЗНО


28.04-04.05. 2022

Урок №5,6" Тіла обертання.Задачі ЗНО"
УВАГА! Тести №1,2,3


Розглянь приклад!

Розв'яжи самостійно!Надіслати електроною поштою


14.04,21.04.2022
Урок №3,4
Куля,сфера їх основні елементи

Приєднайтесь до відео консультації
Передивіться важливі теоритичні відомості
Виконай завдання  Тест№3    https://vseosvita.ua/test/start/grr622
Попередні тести


Готуємося до ЗНО!

ЗАДАЧІ практичної спрямованності(приклади)





07.04.2022
Урок №2
Конус його основні елементи

Приєднайтесь до відео консультації
Передивіться важливі теоритичні відомості
Виконай завдання







Додатковий матеріал

Тест №2https://vseosvita.ua/test/start/dqs059

31.03.2022

Циліндр його основні елементи
Урок №1                                  

Приєднайтесь до відео консультації
Передивіться важливі теоритичні відомості
Виконай завдання

 Основні теоретичні відомості.

Цилиндр – это геометрическое тело, состоящее из двух равных кругов, расположенных в параллельных плоскостях и множества отрезков, соединяющих соответственные точки этих кругов.

  • Почему цилиндр называют телом вращения?

Цилиндр можно получить вращением прямоугольника вокруг одной из его сторон.

  • Назовите виды цилиндров?

Наклонные цилиндры, прямые цилиндры, цилиндрические поверхности

  • Назовите элементы цилиндра.

Основания цилиндра – равные круги, расположенные в параллельных плоскостях

Высота цилиндра - это расстояние между плоскостями его оснований.

Радиус цилиндра – это радиус его основания.

Ось цилиндра – это прямая, проходящая через центры основания цилиндра (ось цилиндра является осью вращения цилиндра).

Образующая цилиндра - это отрезок соединяющий точку окружности верхнего основания с соответственной точкой окружности нижнего основания. Все образующие параллельны оси вращения и имеют одинаковую длину, равную высоте цилиндра.

Образующая цилиндра при вращении вокруг оси образует боковую (цилиндрическую) поверхность цилиндра.

  • Что представляет собой развертка цилиндра?

Разверткой боковой поверхности цилиндра является прямоугольник со сторонами H и C, где H – высота цилиндра, а C – длина окружности основания.

  • Как найти площадь боковой поверхности цилиндра?

Sб = H · C = 2πRH

  • Как найти площадь полной поверхности цилиндра?

Sп = Sб + 2S =  2πR(R + H).

  • Назовите основные виды сечений цилиндра. Какая фигура получается в каждом случае?

Осевое сечение цилиндра – сечение цилиндра плоскостью, проходящей через ось цилиндра (осевое сечение цилиндра является плоскостью симметрии цилиндра). Все осевые сечения цилиндра – равные прямоугольники

Сечение плоскостью, параллельной оси цилиндра. В сечении – прямоугольники.

Сечение плоскостью перпендикулярной оси цилиндра. В сечении круги, равные основанию.

Завдання: Пройди тестування











10.02.2022

Циліндр його основні елементи

Приєднайтесь до відео консультації
Передивіться важливі теоритичні відомості
Виконай завдання



Знайди помилку


 Тестування:  

7 б https://vseosvita.ua/test/start/nrn821  12б     https://vseosvita.ua/test/start/mzj553

                             


03.02.2022

Онлайн урок відбудеться  на платформі Google meet 

Готуємося до ЗНО
Чотирикутники
Приєднайтесь до відео консультації
Передивіться важливі теоритичні відомості з планіметрії(чотирикутники)





№1   https://vseosvita.ua/test/start/frn843
№2    https://vseosvita.ua/test/start/tfd077
Тест №1     8 балів
            №2     12балів  

27.01.2022
Працюємо дистанційно

Онлайн урок відбудеться  на платформі Google meet

 Готуємося до ЗНО

Трикутники
Приєднайтесь до відео консультації
Передивіться важливі теоритичні відомості з планіметрії(трикутники)


Виконайте завдання:
№1 Завдання на встановлення відповідностей


№2 Задачі з коротким розв'язком


https://learningapps.org/4859974
https://learningapps.org/1904986










Контрольна робота 11-А

https://vseosvita.ua/test/start/rwf376

Контрольна робота 11-Б

https://vseosvita.ua/test/start/tqd332

17.12.2021 
піраміда 
Тест відкрито до 19.00  18.12.2021


11.11.2021

Урок №2    Пирамида.Правильна піраміда
1.Подивіться відео уроки
2.Попрацюй з підручником
3.Виконайте малюнок піраміди та назвіть основні її елементи
4. Запишіть означення правильної піраміди
5.Занотуйте основні властивості правильної піраміди.
6.Перевірте свої знання





04.11.2021
Урок №1    Пирамида.Основні елементи піраміди
Повторення: 
Кут між прямою і площиною
Кутом між площиною і прямою, яка перетинає площину і не є перпендикулярною до площини, називають кут між прямою і її проекцією на площину.

Кут між площинами
Кутом між площинами, що перетинаються, називають кут між прямими, проведеними в цих площинах перпендикулярно до лінії їх перетину
1.Подивіться відео уроки
2. Занотуйте означення піраміди
3.Виконайте малюнок піраміди та назвіть основні її елементи
4. Запишіть означення правильної піраміди
5.Занотуйте основні властивості правильної піраміди.
6.Перевірте свої знання




























2020-2021 навчальний рік

26.04-30.04.2021

Онлайн урок відбудеться  на платформі Google meet за розкладом

Урок №9-10   Комбінації фігур у просторі.Куля-піраміда 27.07
Приєднайтесь до онлайн уроку
Запишіть коротенький конспект уроку
Скористайтесь корисними відомостями з теми
Виконайте завдання тестhttps://vseosvita.ua/test/start/sdr674







А. Вписанный шар в пирамиду.

1. В треугольную пирамиду можно вписать шар

2. В пирамиду, у которой в основание можно вписать окружность, центр которой служит основанием высоты пирамиды, можно вписать шар.

Следствие. В любую правильную пирамиду можно вписать шар.

3. Центр шара, вписанного в пирамиду, есть точка пересечения высоты пирамиды с биссектрисой угла, образованного апофемой и ее проекцией на основание.

В. Описанный около пирамиды шар.

1. Около треугольной пирамиды можно описать шар.

2. Если около основания пирамиды можно описать окружность, то около пирамиды можно описать шар.

Следствие. Около любой правильной пирамиды можно описать шар.

3. Центр шара, описанного около пирамиды, лежит в точке пересечения прямой, перпендикулярной основанию пирамиды, проходящей через центр описанной около основания окружности, и плоскости, перпендикулярной любому боковому ребру, проведенной через середину этого ребра.

Следствие. Центр описанной около правильной пирамиды сферы лежит на высоте этой пирамиды.

С. Вписанный в призму шар.

1. Шар можно вписать в прямую призму, если в основание призмы можно вписать окружность, а высота призмы равна диаметру этой окружности.

2. Центр вписанного шара лежит на середине высоты прямой призмы, проходящей через центр окружности, вписанной в основание, а радиус шара равен радиусу окружности, вписанной в основание призмы.

D. Описанный около призмы шар.

1. Около призмы можно описать шар тогда и только тогда, когда призма прямая и около основания можно описать окружность.

2. Центр шара, описанного около прямой призмы, лежит на середине высоты призмы, проведенной через центр окружности, описанной около основания.

Пройдіть тестування     https://vseosvita.ua/test/start/fhz672


20.04.2021

Онлайн урок відбудеться  на платформі Google meet за розкладом

Урок №7-8   Комбінації фігур у просторі.Куля-тіла обертання 20.04-22.04

Передивіться відео уроки
Повторіть властивості кулі та тіл обертання
Розгляньте приклади розв язування задач за посиланням
Виконайте завдання:   Завд.№1  задачи
                                 Завд.№2 тест






Виконайте наступне завдання  №1                                                                                  

1. Якщо кулю радіуса r вписано в циліндр, то площа бічної поверхні циліндра дорівнює:

а) πr2; б) 2πr2; в) 3πr2; г) 4πr2. (1 бал)


2. Відношення об'єму циліндра до об'єму кулі, вписаної в циліндр, до­рівнює:

а) 4 : 3; б) 3 : 2; в) π : 2; г) 2 : 1. (1 бал)


3. Якщо в рівносторонній конус вписано кулю, то відношення площі повної поверхні конуса до площі поверхні кулі дорівнює:

а) 3 : 1; б) 3 : 2 ; в) 9 : 2 ; г) 4 : 1. (2 бали)

4. Якщо в кулю вписано рівносторонній конус, то відношення об'єму кулі до об'єму конуса дорівнює:

а) 3 : 2 ; б) 27 : 5; в) 32 : 27; г) 32 : 9. (2 бали)

5.У конус вписано кулю. Знайдіть об'єм кулі, якщо твірна конуса до­рівнює l і нахилена до площини основи під кутом α. (3бали)

6.   У кулю вписано конус. Площа осьового перерізу конуса дорівнює S, кут між його висотою і твірною дорівнює α. Знайдіть об'єм кулі.(3бали)

Завд.№2 тест  https://vseosvita.ua/test/start/gdw496

13.04.2021

Два письмових завдання:   ТЕСТ
                                               ЗАДАЧІ №1-3

Онлайн урок відбудеться  на платформі Google meet за розкладом

Урок №4-5 Комбінації фігур у просторі.Конус -піраміда
Подивіться відео уроки
Повторіть властивості конуса
Розгляньте приклади розв язків задач
Виконайте завдання

Корисні підказки

  • Конус называется вписанным в пирамиду, если вершины их совпадают, а его основание вписано в основание пирамиды. Причём вписать конус в пирамиду можно только тогда, когда апофемы пирамиды равны между собой (необходимое и достаточное условие);[6]
  • Конус называется описанным около пирамиды, когда их вершины совпадают, а его основание описано около основания пирамиды. Причём описать конус около пирамиды можно только тогда, когда все боковые рёбра пирамиды равны между собой (необходимое и достаточное условие);
  • Высоты у таких конусов и пирамид равны между собой.
  • если центры вписанной и описанной сферы совпадают, то сумма плоских углов при вершине пирамиды равна , а каждый из них соответственно , где n — количество сторон многоугольника основания
  • КУТ при вершині- кут між двома ребрами .ДИВИСЬ ВИДИ КУТІВ ПІРАМІДИ ЗА ПОСИЛАННЯМ    https://images.app.goo.gl/3QnKeHS99cCUfmdt6 








Урок №6   Комбінації фігур у просторі:конус и піраміда
Подивіться відео уроки
розгляньте приклади розв язків задач
Виконайте завдання   

ЗАДАЧА №2

ЗАДАЧА №3


07.04.2021

Комбинации многогранников и тел вращения

Онлайн урок відбудеться  на платформі Google meet за розкладом

Урок №1-2 

Призма, вписанная в цилиндр и описанная около цилиндра. Формула вычисления объема, боковой, полной поверхности цилиндра»

Тела: Призма, пирамида, цилиндр, конус, шар

Какие комбинации геометрических тел возможны?

Шар - конус

Шар - пирамида

Шар - призма....


Полезные подсказки:

Цилиндр называется описанным около призмы, если многоугольники оснований призмы вписаны в окружности оснований цилиндра, а образующие цилиндра являются боковыми рёбрами призмы.

Цилиндр можно описать только около такой прямой призмы, около основания которой можно описать окружность.
Цилиндр всегда можно описать около прямой треугольной призмы, около правильной призмы.

Окружность основания цилиндра описана около многоугольника основания призмы.
Радиус цилиндра — это радиус окружности, описанной около многоугольника основания призмы.

 Центр окружности, описанной около треугольника, является точкой пересечения серединных перпендикуляров к сторонам треугольника.

Центр окружности, описанной около четырёхугольника, является точкой пересечения серединных перпендикуляров к сторонам четырёхугольника. Около четырёхугольника можно описать окружность, если суммы противоположных углов равны 180°.

Цилиндр вписан в призму, если окружности оснований цилиндра вписаны в многоугольники оснований призмы

Цилиндр можно вписать только в такую прямую призму, в многоугольник основания которой можно вписать окружность.
Цилиндр всегда можно вписать в прямую треугольную призму, в правильную призму.

Окружность основания цилиндра вписана в многоугольник основания призмы.

Радиус цилиндра — радиус окружности, вписанной в многоугольник основания призмы.

 Центр вписанной в треугольник окружности находится в точке пересечения биссектрис треугольника.

Центр окружности, вписанной в четырёхугольник, находится в точке пересечения биссектрис четырёхугольника. В четырёхугольник можно вписать окружность, если равны суммы длин противоположных сторон.
 

 !!!  Рисунок создаётся в зависимости от содержания задачи, часто достаточно нарисовать основание комбинаций этих тел, т. к. высота цилиндра равна высоте призмы.


Посмотрите видео урок

https://resh.edu.ru/subject/lesson/4911/train/

Задача
В цилиндр вписана правильная треугольная призма, в которую вписан другой цилиндр, разность площадей боковых поверхностей этих цилиндров равна 40√3 см2Найдите разность объемов цилиндров, если сторона основания призмы равна 24 см 
1.Сделай рисунок 
2.Проанализируй решение
Длина стороны правильного треугольника равна а3=R√3, тогда радиус описанной окружности равен 24: √3=8√3. Радиус вписанной окружности равен 4√3.Зная, что разность площадей боковых поверхностей этих цилиндров равна 40√3 см2 составим уравнение: 40√3π=9 π Н(Rб –rм)=2 π Н (8√3-4√3)=8√3 π Н Следовательно, Н=5 Найдем разность объемов цилиндров: Vб -Vм= π Н (64∙3-16∙3)=720 см
3.Запиши все формулы которые применялись при решении этой задачи.

 ПРОЙДИ ТЕСТИРОВАНИЕ
1.В цилиндр вписан шар. Найдите объем шара, если объем цилиндра равен 60.

2.Цилиндр вписан в куб. Известно, что объем куба равен 40. Найдите объем (V) цилиндра. В ответе запишите V/π.

3.Шар объемом 8 м3 вписан в цилиндр. Найдите объем цилиндра в м3.

4.В основании прямой призмы лежит квадрат со стороной 10. Боковые ребра призмы равны 3/π. Найдите объем цилиндра, описанного около этой призмы.

5.Ребро куба равно 23см. Найдите радиус шара, описанного около этого куба.

6.Найдите площадь боковой поверхности цилиндра, если в цилиндр вписан шар радиуса 4. 

7.В шар вписан конус, причем центр основания конуса совпадает с центром шара . Найдите отношение  объема шара к объему конуса

8.В цилиндрический сосуд с водой бросили свинцовый шар. Радиус основания цилиндра 6 см, радиус шара 3 см. На сколько см поднимется вода в сосуде?

Решения прислать електронной почтой до 09.04.

09.04.2021

Урок №3

Призма, вписанная в цилиндр и описанная около цилиндра. Формула вычисления объема, боковой, полной поверхности цилиндра»

Посмотрите видео урок
Перечитайте полезные подсказки
Реши задание






До 11.04 електронной почтой

π7.В шар вписан конус, причем центр основания конуса совпадает с центром шара . Найдите отношение  объема шара к объему конусаВ цилиндрический сосуд с водой бросили свинцовый шар. Радиус основания цилиндра 6 см, радиус шара 3 см. На сколько см поднимется вода в сосуде?Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 27. Найдите объём цилиндра. Конус описан около правильной четырехугольной пирамиды со стороной основания 6 и высотой 1. Найдите его объем, деленный на 18.03.2021

19.03.2021

Сфера,куля

Передивіться відео урок


Опрацюйте конспект уроку від 15.03 (дивись зошит)
Перейдіть до викнання тестів ЗНО
*Відповіді внести до тестового аркушу,короткі розв' язки записати у зошит.

20. 01.2021

Онлайн урок відбудеться об 11.00 на платформі Google meet.

Урок №5-6 

Правильна піраміда

https://vseosvita.ua/test/start/qtm711

     


15.01.2021

Онлайн урок відбудеться об 11.00 на платформі Google meet.

Урок №3-4

Правильна піраміда

Приєднайтесь до відео консультації
Передивіться відео уроки




ППройдіть тестування за посиланням (час тестування обмежений)

https://vseosvita.ua/test/start/mvw973

 

13.01.2021

Онлайн урок відбудеться об 11.00 на платформі Google meet.

Урок №1-2

Положення висоти у піраміді

Приєднайтесь до відео консультації
Передивіться важливі теоритичні відомості
Передивіться відео уроки
 
Знайдіть формули за допомогою яких можна визначити: площу бокової та повної поверхні піраміди, об єм піраміди. 
Пройдіть тестування за посиланням (час тестування обмежений)

https://vseosvita.ua/test/start/hjn900

Теоритичні відомості

1.                     Если все боковые ребра пирамиды равны или наклонены под одним углом к плоскости основания или образуют равные углы с высотой пирамиды, то основание высоты пирамиды является центром окружности, описанной около основания (и обратно).

2.                       Если все боковые грани пирамиды одинаково наклонены к основанию, то основанием высоты пирамиды является центр окружности, вписанной в основание (и обратно).

 

3.                     Если все боковые грани пирамиды одинаково наклонены к плоскости основания, то основанием высоты пирамиды является точка, равноудаленная от всех прямых, которые содержат стороны основания.

 

4.                      Если только две боковые грани пирамиды (или наклонной призмы)  одинаково наклонены к основанию или общее боковое ребро этих граней образует равные углы со смежными с ним сторонами основания, то это общее боковое ребро проектируется на прямую, содержащую биссектрису угла между смежными с этим ребром сторонами основания (и обратно)

 

5.                     Если только одна боковая грань пирамиды перпендикулярна плоскости основания, то высотой пирамиды будет высота этой грани.

6.                     Если две смежные боковые грани пирамиды перпендикулярны плоскости основания, то высотой пирамиды будет их общее боковое ребро.

 

7.                      Если две не смежные боковые грани пирамиды перпендикулярны плоскости основания, то высотой пирамиды будет отрезок прямой, по которой пересекаются плоскости этих граней.

 

 

1. 


 Про2   24.11.2020

Онлайн урок відбудеться об 11.00 на платформі Google meet.

Приєднайтесь до відео консультації
Передивіться важливі теоритичні відомості з планіметрії
Пройди тестування за посиланням

https://vseosvita.ua/test/start/nss697

11.11.2020

Онлайн урок відбудеться об 11.00 на платформі Google meet.

Пройдіть тестування за посиланням ,розв язки тестових завдань запишіть у зошиті та надішліть електронною поштою

https://vseosvita.ua/test/start/wzn771

04.11.2020

Онлайн урок відбудеться об 11.00 на платформі Google meet.





Тестування!!!

https://vseosvita.ua/test/start/snd463

до 06.11.2020




 22.10.2020

Передивіться відеоурок, перечитайте свій конспект та виконайте завдання тесту


https://forms.gle/Q92d3dBmZwbVLd5D8










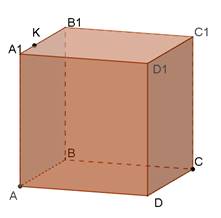
Комментариев нет:

Отправить комментарий

Подписаться на: Комментарии (Atom)