Вчитель математики: Шеремет Валентина Григорівна
МАТЕМАТИКА ДУЖЕ СКЛАДНА ,АЛЕ ЦІКАВА НАУКА. БУДУ РАДА ДОПОМОГТИ ВАМ ЗАЦІКАВИТИСЯ ВИВЧЕННЯМ МАТЕМАТИКИ,ЗРОЗУМІТИ ЇЇ КРАСУ,ТА З ЛЕГКІСТЮ ПОДОЛАТИ УСІ ТРУДНОЩІ НА ШЛЯХУ ДО МАТЕМАТИЧНИХ НАУК.
Виконуйте завдання : здати до 27.10.23, надіслати електронною поштою
1. Якщо р = 2k, k 
Z, то
функція у = х2k. Якщо k = 1, то ця функція має вигляд у = х2.
Згадаємо її основні властивості. Функція у = х2:
-
визначена для будь-якого
дійсного х;
-
додатна при х ≠ 0 і дорівнює 0 при х = 0;
-
приймає всі невід'ємні
значення;
-
парна (графік симетричний
відносно осі OY);
-
спадає, якщо х є (-
; 0] і зростає, якщо х є [0; +). Такі саме властивості має. функція у = х2k
-
2. Якщо р = 1, то
функція має вигляд у = х (графік — пряма, що проходить через
початок координат і ділить перший і третій координатний кути пополам). Якщо р
= 3, то ця функція має вигляд у
= х3. Функція у = х3:
-
визначена для будь-якого
дійсного х;
-
додатна при х > 0,
від'ємна при х < 0 і дорівнює 0 при х = 0;
-
зростаюча;
-
приймає всі дійсні значення;
-
непарна (графік симетричний
відносно початку координат), Такі самі властивості має степенева функція у =
х2k+1, k N
Завдання:
Виконуйте завдання:
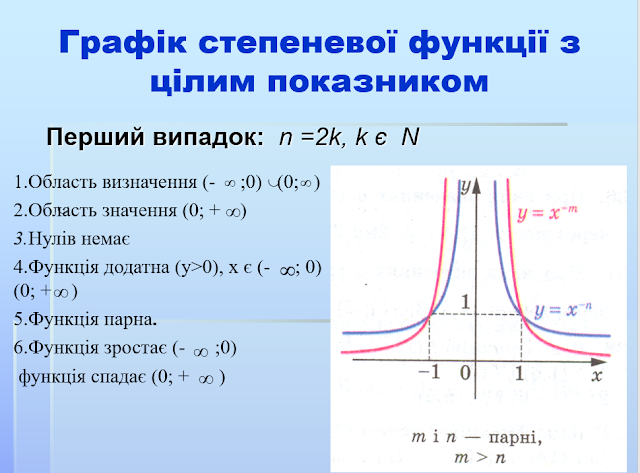
Елементарні функції:
1. Лінійна функція y=kx+b, k,b- числа. Графік – пряма. Для побудови потрібно дві точки. k=tgα, де α –кут між прямою і додатним напрямом осі Ох, (0;b) –точка перетину прямої і осі Оу
| k>0 | k<0 |
 |  |
Окремі випадки лінійної функції
| b=0, y=kx пряма пропорційність | k=0, y= b |
 |  |
| проходить через початок координат | пряма паралельна осі Ох |
2. Обернена пропорційність 
Графік гіпербола.
| k>0 | k<0 |
 |  |
3. Квадратична функція ax2+bx+c, a,b,c-числа, a≠0.
Графік парабола.
y=x2 Приклад 8. Розв’яжіть систему рівнянь способом підстановки
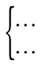
Якщо доводиться знаходити спільні розв'язки двох або більшої кількості нерівностей з однією і тією самою змінною, то кажуть, що ці нерівності утворюють систему нерівностей. Систему нерівностей позначають фігурною дужкою:
Розв'язок системи нерівностей – це значення змінної, яке задовольняє кожну нерівність системи. Розв'язати систему нерівностей – означає знайти всі її розв'язки або показати, що вона їх немає.
|
Приклад 1. Розв'яжемо систему нерівностей
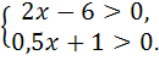
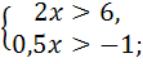
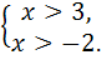
Розв'язок кожної з нерівностей системи є числовим проміжком, відповідно (3; +∞) і (-2; +∞).
Запис (3; +∞) (-2; +∞) означає переріз, тобто спільну частину даних проміжків.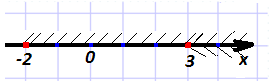 
Розв'язком нерівності є проміжок (3; +∞).
Приклад 2. Розв'язати систему нерівностей
Розв'язання:
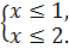
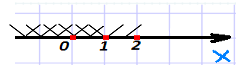або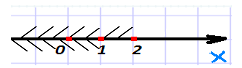 
З рисунка видно, що розв'язком системи є х≤1, тобто х(-∞; 1]
Приклад 3. Розв'язати систему нерівностей
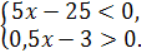
Розв'язання:
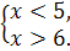
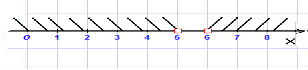
Очевидно, що числові проміжки (-∞; 5) і (6; ∞) не мають жодного спільного числа. Тому система нерівностей не має розв'язку.
У такому випадку кажуть, що переріз даних числових проміжків – порожня множина, яку позначають знаком .
Системи рівнянь
- Повторимо для початку , як розв’язувати дані системи графічним способом і способом підстановки Якщо треба знайти спільний розв’язок двох рівнянь із двома змінними, то кажуть, що ці рівняння утворюють систему рівнянь. Позначення: 2. Розв’язком системи рівнянь із двома змінними називають пару значень змінних, при яких кожне рівняння перетворюється на правильну числову рівність. Розв’язати систему рівнянь означає знайти всі її розв’язки або довести, що їх немає. II. Розв’язування систем лінійних рівнянь. 1) Спосіб підстановки. 2) Спосіб додавання. 3)Графічний спосіб 3. Щоб розв’язати систему лінійних рівнянь із двома змінними, можна скористатися графіками рівнянь. Такий спосіб називається графічним способом розв’язування систем рівнянь. ЩЩоб розв’язати систему рівнянь графічним способом, треба: 1. виконати рівносильні перетворення системи так, щоб було зручно побудувати гргафіки рівнянь системи; 2. побудувати графіки; 3. знайти координати точок (точки) перетину побудованих ліній. Ці координати і є рррозв’язками (розв’язком) системи рівнянь. Приклад. Розв’яжіть графічно систему рівнянь
M(1;2) — точка перетину графіків рівнянь (рис. 1).
Рис. 1 Алгоритм! 1. Побудуємо графіки рівнянь системи в одній координатній площині. 2. Знайдемо координати точки перетину графіків рівнянь. 3. Якщо координати точки перетину цілі числа, то треба виконати перевірку, якщо ні, то дати приблизну відповідь. Отже, графіком кожного рівняння системи лінійних рівнянь із двома змінними є пряма. Якщо прямі перетинаються, то система має єдиний розв’язок; якщо прямі не перетинаються, то система не має розв’язків; якщо прямі збігаються, то система має безліч розв’язків. ЗаЗауваження. Графічний спосіб розв’язування систем рівнянь не є універсальним, оскільки нене завжди розв’язком системи є пара цілих чисел. Іноді важко точно встановити кокоординати точки перетину побудованих графіків функцій, можливо лише вказати нанайближенні значення. Тому, як правило, використовують алгебрагічні способи ророзв’язування систем рівнянь: спосіб підстановки, додавання. СпСособом підстановки систему двох рівнянь із двома змінними розв’язують за таким порядком: 1. з одного рівняння системи виражаємо одну зі змінних через другу змінну і відомі величини; 2. знайдене значення підставляємо в друге рівняння системи, одержуємо рівняння відносно другої змінної; 3. розв’язуємо одержане рівняння і знаходимо значення цієї змінної; 4. підставляючи знайдене значення у вираз для першої змінної, одержуємо відповідне її значення; 5. записуємо відповідь. Спосіб підстановки:
Спосіб додавання:
| ||||||||||||||
| ||||||||||||||
1. Схема розв’язування нерівності методом інтервалів :
1. Привести нерівність до такого виду, де в лівій частині знаходиться функція,
а в правій 0.
2. Знайти область визначення функції.
3. Знайти нулі функції, тобто - вирішити рівняння, х1 = m, x2 = n.
4. На числову пряму нанесемо область визначення функції і за допомогою нулів розіб’ємо її (область визначення) на інтервали.
5. Визначити знаки функції на отриманих інтервалах.
6. Вибрати інтервали, де функція набуває необхідних значень і записати відповідь.
2. Застосування методу інтервалів на прикладах.
Розв’яжемо нерівність (х + 2)(х - 3)(х - 5) >0.
2.Область визначення функції — множина дійсних чисел.
3.Нулі функції: х1=-2, х2=3, х3=5.
4.Нулі розбивають область визначення на чотири проміжки: ( -
5. Позначимо на координатній прямій нулі функції та її знаки на кожному з проміжків.
6. Виберемо проміжки в залежності від знаку нерівності.
7.Відповідь: (-2; 3) (5; +
!!! На кожному з проміжків функція зберігає знак, а після переходу через нулі її знак змінюється(непарка кратність), не змінюється ( парна кратність).
У такий спосіб можна знайти знаки функції виду
f(x) = (х – х1)(х – х2)(х – х3)…(х - хn)
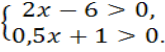
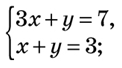
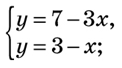
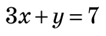
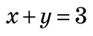
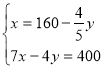
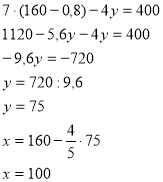
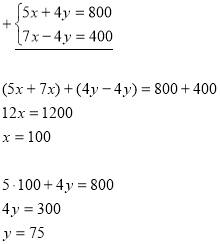
Комментариев нет:
Отправить комментарий