2023-2024 навчальний рік
1.Онлайн консультація на платформі Google meet
за розкладом!
2.Консультації та завдання на блогу
Працюємо у гугол класі!код приєднання
https://classroom.google.com/c/NjIyMzc5Mzk1MDA4?cjc=yjucble
23.10-27.10.23
Піраміда, її основні елементи Приєднайтеся до уроків на платформі Google meet за розкладом Попрацюйте з теоритичними відомостями Передивіться відео уроки
Теоритичні відомості
Означення. Піраміда — це багатогранна об'ємна фігура, яка обмежена плоским багатокутником (основа), та трикутниками, що мають спільну вершину, яка не лежить в площині основи.
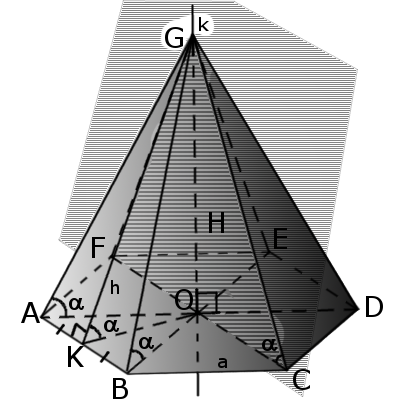 |
| Рис.1 |
Об'єм та площа поверхні піраміди
Формула. Об'єм піраміди через площу основу та висоту:V = 1 SоснH 3
Означення. Бічна поверхня піраміди - це сукупна площа всіх бокових граней піраміди.Означення. Повна поверхня піраміди - це сукупність площ бічної поверхні та основи піраміди.Формула. Площа бічної поверхні правильної піраміди через периметр основи та апофему:Sb = 1 ph 2
| V = | 1 | SоснH |
| 3 |
| Sb = | 1 | ph |
| 2 |
Властивості піраміди
Якшо всі бічні ребра рівні, то навколо основи піраміди можна описати коло, та вершина піраміди проецюється в його центр.Якшо всі бічні ребра рівні, то бічні ребра утворюють з площиною основи рівні кути.Бічні ребра рівні, якщо бічні ребра утворюють з площиною основи рівні кути або якщо навколо основи піраміди можна описати коло та вершина піраміди проецюється в його центр.Якшо бічні грані нахилені до площини основи під одним кутом, то в основу піраміди можна вписати коло, та вершина пірамиди проецюється в його центр.Якшо бічні грані нахилені до площини основи під одним кутом, то высоти бічих граней рівні.
Властивості правильної піраміди
1. Вершина піраміди однаково віддалені від усіх кутів основи.2. Всі бічні ребра рівні.3. Всі бічні ребра нахилені під однаковим кутом до основи.4. Апофеми всіх бічних граней рівні.5. Площі всіх бічних граней рівні.6. Всі грані мають однакові двогранні (плоскі) кути.7. Навколо піраміди можна описати сферу. Центром описаної сфери буде точка перетину перпендикулярів, які проходять через середину ребер.8. В піраміду можна вписати сферу. Центром вписаної сфери буде точка перетину бісектрис, які виходять з кута між ребром та основою.9. Якщо центр вписаної сфери співпадає з центром описаної сфери, то сума плоских кутів при вершині дорівнює π, або один кут дорівнює π/n, де n - це кількість кутів в основі піраміди.
Тестування: https://vseosvita.ua/test/start/hlx596
Тривалісь тесту 20 чвилин, перед виконанням попрацюй з теоритичними відомостями
16.10-20.10.23 Приєднайтеся до уроків на платформі Google meet за розкладом Попрацюйте з теоритичними відомостями Передивіться відео уроки
20 .10 Контрольна робота 14.00-15.00
- призма — це багатогранна об’ємна фігура, яка складається з двох однакових плоских багатокутників (основ), що знаходяться у двох паралельних площинах, а інші грані (бічні грані) – паралелограми, що мають спільні сторони з цими багатокутниками.
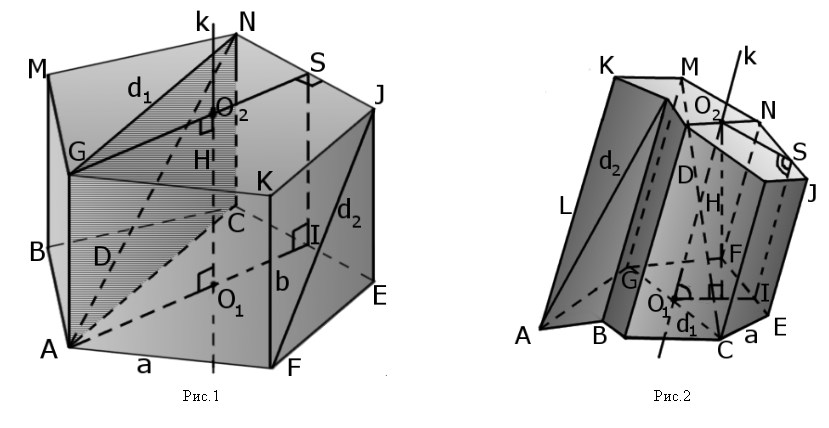
- Основи призми – дві грані, які є рівними паралельними плоскими багатокутниками (ABCEF, GMNJK).
- Бічні грані призми – всі інші грані за винятком основ.
- Бічна поверхня призми – сукупність всіх бічних граней призми.
- Поверхня призми – це сукупність поверхонь двох основ і бічної поверхні.
- Бічне ребро призми – спільна сторона двох бічних граней.
- Висота – це перпендикуляр, який з’єднує дві основи призми під прямим кутом.
- Діагональ основи призми – це відрізок, що з’єднує дві не сусідні вершини, що належать цій же основі.
- Діагональ бічної грані призми – це відрізок, що з’єднує дві протилежні вершини, що лежать на одній бічній грані однак належать до різних основ.
- Діагональ призми (AN) – це відрізок, що з’єднує дві вершини, що лежать на різних основах але не лежать на одній бічній стороні.
- Діагональний перетин – це перетин призми площиною, що проходить через діагональ основи призми і бічне ребро. Трикутна призма (в основі призми, трикутники) не має діагональних перерізів.
- Перпендикулярний переріз – це перетин призми площиною, що перетинає бічні ребра призми під прямим кутом.
- Пряма призма – це призма, в якій всі бічні грані перпендикулярні до основи. Висота дорівнює довжині бічного ребра.
- похила призма – це призма, у якої бічні грані не перпендикулярні до основи.
- Правильна призма – це призма, в якій основи є правильними многокутниками. Правильна призма може бути як прямою, так і похилою
- Основні властивості призми
- Основи призми – рівні многокутники.
- Бічні грані призми – паралелограми.
- Бічні ребра призми паралельні і рівні між собою.
- Перпендикулярний переріз перпендикулярній всім бічним ребрам і бічним граням.
- Висота прямої призми дорівнює довжині бічного ребра.
- Висота похилої призми завжди менше довжини ребра.
- У прямій призмі гранями можуть бути прямими або квадратами.
Площадь поверхности призмы
Поверхность многогранника состоит из конечного числа многоугольников (граней). Площадь поверхности многогранника есть сумма площадей всех его граней. Площадь поверхности призм (Sпр) равна сумме площадей ее боковых граней (площади боковой поверхности Sбок) и площадей двух оснований (2Sосн) - равных многоугольников:
Sпр=Sбок+2Sосн.
Теорема. Площадь боковой поверхности призмы равна произведению периметра ее перпендикулярного сечения и длины бокового ребра.
Об'єм
V=Sосн H
Відео уроки
- призма — це багатогранна об’ємна фігура, яка складається з двох однакових плоских багатокутників (основ), що знаходяться у двох паралельних площинах, а інші грані (бічні грані) – паралелограми, що мають спільні сторони з цими багатокутниками.

- Основи призми – дві грані, які є рівними паралельними плоскими багатокутниками (ABCEF, GMNJK).
- Бічні грані призми – всі інші грані за винятком основ.
- Бічна поверхня призми – сукупність всіх бічних граней призми.
- Поверхня призми – це сукупність поверхонь двох основ і бічної поверхні.
- Бічне ребро призми – спільна сторона двох бічних граней.
- Висота – це перпендикуляр, який з’єднує дві основи призми під прямим кутом.
- Діагональ основи призми – це відрізок, що з’єднує дві не сусідні вершини, що належать цій же основі.
- Діагональ бічної грані призми – це відрізок, що з’єднує дві протилежні вершини, що лежать на одній бічній грані однак належать до різних основ.
- Діагональ призми (AN) – це відрізок, що з’єднує дві вершини, що лежать на різних основах але не лежать на одній бічній стороні.
- Діагональний перетин – це перетин призми площиною, що проходить через діагональ основи призми і бічне ребро. Трикутна призма (в основі призми, трикутники) не має діагональних перерізів.
- Перпендикулярний переріз – це перетин призми площиною, що перетинає бічні ребра призми під прямим кутом.
- Пряма призма – це призма, в якій всі бічні грані перпендикулярні до основи. Висота дорівнює довжині бічного ребра.
- похила призма – це призма, у якої бічні грані не перпендикулярні до основи.
- Правильна призма – це призма, в якій основи є правильними многокутниками. Правильна призма може бути як прямою, так і похилою
- Основні властивості призми
- Основи призми – рівні многокутники.
- Бічні грані призми – паралелограми.
- Бічні ребра призми паралельні і рівні між собою.
- Перпендикулярний переріз перпендикулярній всім бічним ребрам і бічним граням.
- Висота прямої призми дорівнює довжині бічного ребра.
- Висота похилої призми завжди менше довжини ребра.
- У прямій призмі гранями можуть бути прямими або квадратами.
Площадь поверхности призмы
Поверхность многогранника состоит из конечного числа многоугольников (граней). Площадь поверхности многогранника есть сумма площадей всех его граней. Площадь поверхности призм (Sпр) равна сумме площадей ее боковых граней (площади боковой поверхности Sбок) и площадей двух оснований (2Sосн) - равных многоугольников:
Sпр=Sбок+2Sосн.
Теорема. Площадь боковой поверхности призмы равна произведению периметра ее перпендикулярного сечения и длины бокового ребра.
Об'єм
V=Sосн H
Відео уроки
Завдання: №1 Розв'язати задачі (до 20.10.23)
№2 Контрольна робота 20.10 з 13.00 до 14.00
09.10-13.10.23
Побудова перерізів многогранників.Метод сліду. Приєднайтеся до уроків на платформі Google meet за розкладом Попрацюйте з теоритичними відомостями Передивіться відео уроки
Приклади
Відео уроки
Завдання: всі завдання надіслати електронною поштою до 15.10№1 Побудувати переріз малюнок 3.12, 3.14, 3.18
02.10-06.10.23
Приєднайтеся до уроків на платформі Google meet за розкладомПопрацюйте з теоритичними відомостямиПередивіться відео урокиВиконуйте домашне завдання: Відео уроки
Приклади задач
Завдання№1 Оберіть завдання , та виконайте його.Задачи :1-3 7 б1.Обчислити площу повної поверхні куба з ребром 6 см.
2.Обчислити бічну поверхню паралелепіпеда,якщо його виміри дорівнюють
а=5 см, b=8 см, h=10 см.
3.Діагональ правильної чотирикутної призми дорівнює 20 см .Знайти
діагональ бічної грані призми,якщо сторона основи дорівнює 12 см.
Задачі 1-4 10 б
1.Обчислити площу повної поверхні куба з ребром 6 см.
2.Обчислити бічну поверхню паралелепіпеда,якщо його виміри дорівнюють
а=5 см, b=8 см, h=10 см.
3.Діагональ правильної чотирикутної призми дорівнює 20 см .Знайти
діагональ бічної грані призми,якщо сторона основи дорівнює 12 см.
Задачі 1-4 10 б
№2 Перевірочна контрольна робота здати 06.10 до 22.00
Завдання 1-3 5 б
А) 6см;
Б) 7см; В) 8см; Г) 11см; Д)
2. Знайти площу бічної поверхні прямої призми,
бічне ребро якої дорівнює 10см, а в основі лежить ромб із діагоналями 6см і
8см.
А) 100см2; Б) 200см2; В)
240см2; Г) 360см2; Д) 540см2.
3. Якщо діагональ бічної грані правильної
трикутної призми дорівнює d
А) d cos a
Завдання 4- 2,5
б 5- 2,5 б
Максимальна оцінка 10 б
25.09-29.09.23
Приєднайтеся до уроків на платформі Google meet за розкладомПопрацюйте з теоритичними відомостямиПередивіться відео урокиВиконуйте домашне завдання:
Приклад оформлення розв'язку задачі
Завдання:
№1 Зроби малюнок та розв'яжи задачу В основі прямого паралелепіпеда лежить ромб, менша діагональ якого дорівнює d. Більша діагональ
паралелепіпеда дорівнює 2d і утворює кут α з основою паралелепіпеда.
Знайдіть:
а) довжину бічного ребра; (1 бали)
б) більшу діагональ основи; (2 бали)
в) площу основи паралелепіпеда; (1 бали)
г) довжину сторони основи; (2 бали)
д) площу бічної поверхні паралелепіпеда; (2 бали)
е) кут нахилу меншої діагоналі паралелепіпеда до площини основи. (2
бали)
№2 тестування https://vseosvita.ua/test/start/oxo258
18.09-22.09.23
Приєднайтеся до уроків на платформі Google meet за розкладомПопрацюйте з теоритичними відомостямиПередивіться відео урокиВиконуйте домашне завдання:№1 Відповіді на запитання№2 тестування
№3 самостійна робота (до завдань 1-6 дати короткі розв'язки) 7,8 повні розв'язкиПаралелепіпеди.

Властивості
· Паралелепіпед симетричний щодо середини його діагоналі.
· Будь-який відрізок з кінцями, що належать поверхні паралелепіпеда і проходить через середину його діагоналі, ділиться нею навпіл; зокрема, всі діагоналі паралелепіпеда перетинаються в одній точці і діляться нею навпіл.
· Протилежні грані паралелепіпеда паралельні та рівні.
· Квадрат довжини діагоналі прямокутного паралелепіпеда дорівнює сумі квадратів трьох його вимірювань
Приклади розв'язування задач
Завдання:
№1 відповіді на запитання( усно)

Властивості
· Паралелепіпед симетричний щодо середини його діагоналі.
· Будь-який відрізок з кінцями, що належать поверхні паралелепіпеда і проходить через середину його діагоналі, ділиться нею навпіл; зокрема, всі діагоналі паралелепіпеда перетинаються в одній точці і діляться нею навпіл.
· Протилежні грані паралелепіпеда паралельні та рівні.
· Квадрат довжини діагоналі прямокутного паралелепіпеда дорівнює сумі квадратів трьох його вимірювань
Приклади розв'язування задач
Завдання:
№1 відповіді на запитання( усно)
1. Відомо, що тільки дві бічні грані паралелепіпеда перпендикулярні до основи. Якого виду паралелепіпед?
2. Скільки бічних граней прямокутної форми може мати паралелепіпед?
3. Чи можливий паралелепіпед, у якого лише одна бічна грань:
1) перпендикулярна до основи;
2) має форму прямокутника.
4. У прямому паралелепіпеді всі діагоналі рівні. Чи є він прямокутним?
5. Чи правильно, що у прямому паралелепіпеді діагональні перерізи перпендикулярні до площин основи?
6. Сформулюйте теорему, обернену до теореми про квадрат діагоналі прямокутного паралелепіпеда.
7. Які додаткові ознаки відрізняють куб від прямокутного паралелепіпеда?
8. Чи буде кубом паралелепіпед, у якому рівні всі ребра при одній з вершин?
9. Сформулюйте теорему про квадрат діагоналі прямокутного паралелепіпеда для випадку куба.
№2 тестування https://vseosvita.ua/test/start/oha927
№3 самостійна робота (до завдань 1-6 дати короткі розв'язки) 7,8 повні розв'язки
11.09-15.09.2023
Теоритичні відомості
Визначення призми
- призма — це багатогранна об’ємна фігура, яка складається з двох однакових плоских багатокутників (основ), що знаходяться у двох паралельних площинах, а інші грані (бічні грані) – паралелограми, що мають спільні сторони з цими багатокутниками.

- Основи призми – дві грані, які є рівними паралельними плоскими багатокутниками (ABCEF, GMNJK).
- Бічні грані призми – всі інші грані за винятком основ.
- Бічна поверхня призми – сукупність всіх бічних граней призми.
- Поверхня призми – це сукупність поверхонь двох основ і бічної поверхні.
- Бічне ребро призми – спільна сторона двох бічних граней.
- Висота – це перпендикуляр, який з’єднує дві основи призми під прямим кутом.
- Діагональ основи призми – це відрізок, що з’єднує дві не сусідні вершини, що належать цій же основі.
- Діагональ бічної грані призми – це відрізок, що з’єднує дві протилежні вершини, що лежать на одній бічній грані однак належать до різних основ.
- Діагональ призми (AN) – це відрізок, що з’єднує дві вершини, що лежать на різних основах але не лежать на одній бічній стороні.
- Діагональний перетин – це перетин призми площиною, що проходить через діагональ основи призми і бічне ребро. Трикутна призма (в основі призми, трикутники) не має діагональних перерізів.
- Перпендикулярний переріз – це перетин призми площиною, що перетинає бічні ребра призми під прямим кутом.
- Пряма призма – це призма, в якій всі бічні грані перпендикулярні до основи. Висота дорівнює довжині бічного ребра.
- похила призма – це призма, у якої бічні грані не перпендикулярні до основи.
- Правильна призма – це призма, в якій основи є правильними многокутниками. Правильна призма може бути як прямою, так і похилою
- Основні властивості призми
- Основи призми – рівні многокутники.
- Бічні грані призми – паралелограми.
- Бічні ребра призми паралельні і рівні між собою.
- Перпендикулярний переріз перпендикулярній всім бічним ребрам і бічним граням.
- Висота прямої призми дорівнює довжині бічного ребра.
- Висота похилої призми завжди менше довжини ребра.
- У прямій призмі гранями можуть бути прямими або квадратами.
Площадь поверхности призмы
Поверхность многогранника состоит из конечного числа многоугольников (граней). Площадь поверхности многогранника есть сумма площадей всех его граней. Площадь поверхности призм (Sпр) равна сумме площадей ее боковых граней (площади боковой поверхности Sбок) и площадей двух оснований (2Sосн) - равных многоугольников:
Sпр=Sбок+2Sосн.
Теорема. Площадь боковой поверхности призмы равна произведению периметра ее перпендикулярного сечения и длины бокового ребра.
Об'єм
V=Sосн H
Відео уроки
ДОМАШНЕ ЗАВДАННЯ
№1 Пройдить тестування(тривалість тесту 20 хвилин)
https://vseosvita.ua/test/start/lcp842
№2




















Комментариев нет:
Отправить комментарий